[Python 3] BOJ - 20530 "양분"

 # 문제 링크

https://www.acmicpc.net/problem/20530

20530번: 양분

 

 # 풀이

 개인적으로 이 문제의 핵심은 사이클 검출이라고 생각한다.

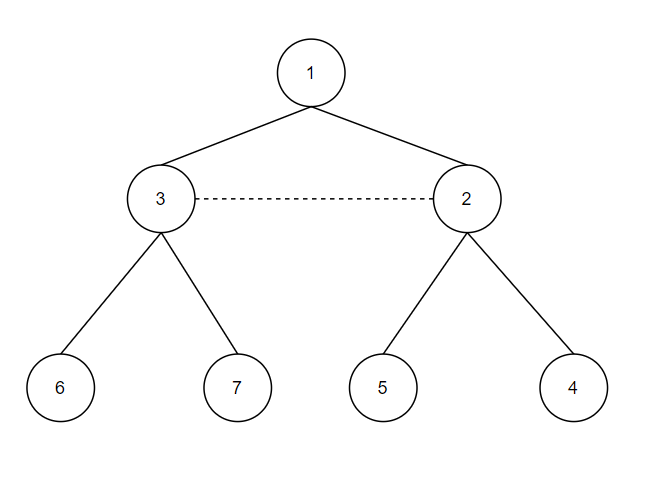
<그림 1. 예제 입력 1의 경우>

 위 그림 1은 예제 입력 1의 경우를 나타낸 것이다. 이 때, 점선을 빼고 생각하면 이 그래프는 트리임이 자명하다. 트리의 성질로 인해 정점 수가 N개라면, 간선 수는 N-1개이다. 또한 문제에서 제시하는 두 조건, 중복 간선과 루프 간선이 없음을 트리는 만족한다. 그런데 문제에서는 입력으로 주어지는 그래프의 간선의 수가 N개라고 정의했으므로 위 그림 1의 점선에 대응되는 종류의 간선이 하나가 추가가 됨을 알 수 있다. 따라서, 입력으로 주어지는 그래프에는 무조건 사이클이 단 하나가 있다. 왜냐하면 트리의 성질에 의해 임의의 서로 다른 두 간선에는 무조건 경로가 있기 때문이다. 그러한 경로에서 양 끝점에 간선 하나를 추가하면 사이클이 생기는 것은 자명하다.

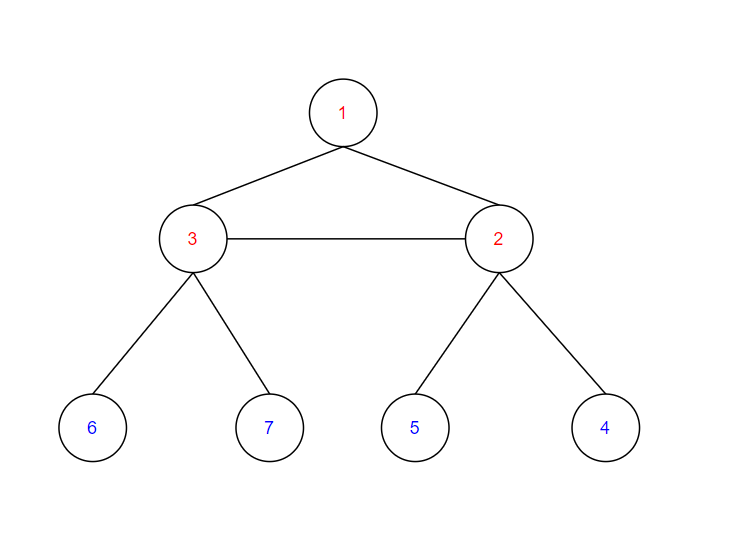
<그림 2. 예제 입력 1의 경우>

 위 그림 2는 정점이 사이클에 속하는지 여부에 따른 그림이다. 빨간색으로 적힌 노드는 사이클의 일부, 파란색으로 적힌 노드는 사이클의 일부가 아닌 노드들이다. 이 때, 임의의 두 점을 뽑게 된다면 경우는 세 가지로 나뉘게 된다. 첫번째로 사이클 내부의 두 정점이 뽑히는 경우와, 두번째로 사이클 내부의 정점 하나와 사이클이 아닌 정점 하나, 마지막으로 둘 다 사이클이 아닌 정점을 뽑는 경우이다.

 첫번째 경우를 생각해보자. 예를 들어 1과 3의 경우를 생각해보자. 그렇다면 경로의 수는 (1,3)과 (1,2,3)이 됨을 알 수 있다. 즉, 끝점을 기준으로 왼쪽 혹은 오른쪽 두 가지 경우밖에 없음을 알 수 있다. 따라서 첫번째 경우라면 2가 답이 된다.

 두번째 경우를 생각해보자. 예를 들어 2와 7의 경우를 생각해보자. 그렇다면 경로의 수는 (2,3,7)과 (2,1,3,7)이 됨을 알 수 있다. 이 경우 7과 가장 가까운 사이클 내부의 정점은 3이기 때문에 사실상 2에서 3의 경로 수와 같아진다. 그렇다면 두번째 경우는 모두 답이 2가 될까? 그렇지 않다. 예를 들어 3과 7을 생각해보자. 경로는 (3,7)로 무조건 하나가 된다. 

 마지막으로 세 번째 경우를 생각해보자. 예를 들어 6과 5를 생각해보자. 두번째 경우의 논리에 의해 사실상 6과 가장 가까운 사이클 정점인 3과 5와 가장 가까운 사이클 정점인 2 사이의 경로의 수와 같아진다. 따라서 답은 2이다. 그렇다면 세번째 경우는 모두 답이 2가 될까? 그렇지 않다. 예를 들어 6과 7을 생각해보자. 이 때는 경로가 (6,3,7)로 단 하나가 됨을 알 수 있다.

<그림 3. 예제 입력 1의 경우>

 위 그림 3은 그림 2에서 생각할 수 있는 경우를 일반화한 그림이다. 이 때 각 박스는 사이클 내부의 정점별로 사이클 내부의 정점이 아닌 정점들과 자신으로 이루어진 연결요소이다. 따라서, 각 박스는 트리가 됨은 자명하다. 그런데 트리의 경우는 트리 내부의 임의의 두 정점 간의 경로의 수는 하나이다. 따라서 쿼리로 들어오는 두 정점이 같은 박스라면 답은 1이고, 아니라면 답은 2가 됨을 알 수 있다

  

 # 코드

import sys

# 재귀깊이해제
sys.setrecursionlimit(300000)

# go : 현재 정점이 now고 사이클의 끝점이 base일 때 사이클 내부의 정점을 검출하는 함수
def go(now, base):
    while now != base:
        is_cycle[now] = True
        now = parent[now]
    is_cycle[base] = True

# dfs : 현재 정점이 now이고 이전 정점이 prev일 때, 사이클의 여부를 리턴하는 함수
def dfs(now, prev):
    # 방문 표시
    check[now] = True
    for i in adj[now]:
        if i == prev:
            continue
        if not check[i]:
            # 방문하지 않은 정점이라면 현재 정점이 부모 정점이 된다
            parent[i] = now
            # 사이클이 검출되면 계속 True를 리턴
            res = dfs(i, now)
            if res:
                return res
        # 현재 정점이 사이클의 끝점이라면 go 함수 호출 후 사이클 검출의 의미로 True 리턴
        elif not fin[i]:
            go(now, i)
            return True
    # 현재 정점 종료 표시
    fin[now] = True
    return False

# get_tree_num : 현재 정점이 now고 이전 정점이 prev일 때 트리 번호를 채우는 함수
def get_tree_num(now, prev):
    tr_num[now] = num
    for i in adj[now]:
        if i == prev:
            continue
        if is_cycle[i]:
            continue
        if tr_num[i] == -1:
            get_tree_num(i, now)

# 입력부
n, q = map(int, sys.stdin.readline().split())

# 인접 리스트
adj = [[] for _ in range(n + 1)]
# is_cycle : 현재 정점이 사이클인지 아닌지 저장하는 리스트
is_cycle = [False] * (n + 1)
# check : 현재 정점을 방문했는지 아닌지 저장하는 리스트
check = [False] * (n + 1)
# fin : 현재 정점의 방문이 끝났는지 아닌지 저장하는 리스트
fin = [False] * (n + 1)
# parent : 현재 정점의 부모 정점을 저장하는 리스트
parent = [-1] * (n + 1)

for i in range(1, n + 1):
    a, b = map(int, sys.stdin.readline().split())
    adj[a].append(b)
    adj[b].append(a)

# 사이클 검출
dfs(1, -1)

# tr_num : 현재 정점의 트리 번호를 저장하는 리스트
tr_num = [-1] * (n + 1)
# num : 현재 트리 번호
num = 0
for i in range(1, n + 1):
    # 사이클 내부의 각 정점에 대해 트리 번호를 채움
    if is_cycle[i]:
        no_cycle(i, -1)
        num += 1

# 트리 번호가 같으면 1, 아니면 2 출력
for _ in range(q):
    a, b = map(int, sys.stdin.readline().split())
    if tr_num[a] == tr_num[b]:
        print(1)
    else:
        print(2)