Atcoder Beginner Contest 267 후기

A. Saturday

 월요일부터 금요일까지 임의의 요일이 입력될 때, 토요일까지 몇일이 남았는지 출력하는 문제이다

import sys

cache = {"Monday" : 5, "Tuesday" : 4, "Wednesday" : 3, "Thursday" : 2, "Friday" : 1}
n = sys.stdin.readline().rstrip()
print(cache[n])

 

B. Split?

 단순 구현 문제이다. 문제에서 요구한 조건에 따라 split 여부를 구해주면 된다. n이 매우 작기 때문에 웬만한 브루트포스로도 충분하다

import sys

n = sys.stdin.readline().rstrip()

# cache : 각 기둥이 key, 담고 있는 핀 번호의 배열을 value로 하는 dictionary
cache = {1 : [6], 2 : [3], 3 : [7, 1], 4 : [4, 0], 5 : [8, 2], 6 : [5], 7 : [9]}

# alive : 모든 핀이 쓰러지지 않은 기둥의 번호를 저장하는 배열
alive = []
# empty : 모든 핀이 쓰러진 기둥의 번호를 저장하는 배열
empty = []

# 1번부터 7번 기둥까지 순회하면서 모든 핀이 쓰러졌는지 여부에 따라 alive, empty 배열에 저장
for i in range(1, 8):
    cnt = 0
    for j in cache[i]:
        if n[j] == '1':
            alive.append(i)
            break
        else:
            cnt += 1
    if cnt == len(cache[i]):
        empty.append(i)
        
# 문제의 조건에 따라 1번 핀이 쓰러지지 않는 경우 No 출력
if n[0] == '1':
    print('No')
else:
    # 1번 핀이 쓰러진 경우
    alive.sort()
    for i in range(len(alive)):
        for j in range(i + 1, len(alive)):
            # cnt : 현재 i번째 기둥과 j번째 기둥 사이의 남은 기둥 수
            cnt = alive[j] - alive[i] - 1
            temp = 0
            # i번 기둥과 j번 기둥 사이에 모든 기둥을 순회하면서 모든 핀이 쓰러진 기둥의 갯수를 확인
            for k in range(alive[i] + 1, alive[j]):
                if k in empty:
                    temp += 1
            # i와 j번 기둥 사이에 모든 기둥이 empty에 속한다면 Yes 출력
            if cnt > 0 and cnt == temp:
                print('Yes')
                sys.exit(0)
    # 조건을 만족하지 않는 쌍이 하나라도 있으면 No 출력
    print('No')

 

C. Index × A(Continuous ver.)

 특정 배열이 주어지고, 길이가 m인 연속된 부분 배열들 중에서, $ \sum_{i=1}^{m} i * A_{i} $을 최대로 하는 부분 배열을 찾는 문제이다. n과 m이 20만이기 때문에 단순한 $O(N^2)$으로는 시간초과를 피할 수 없다.

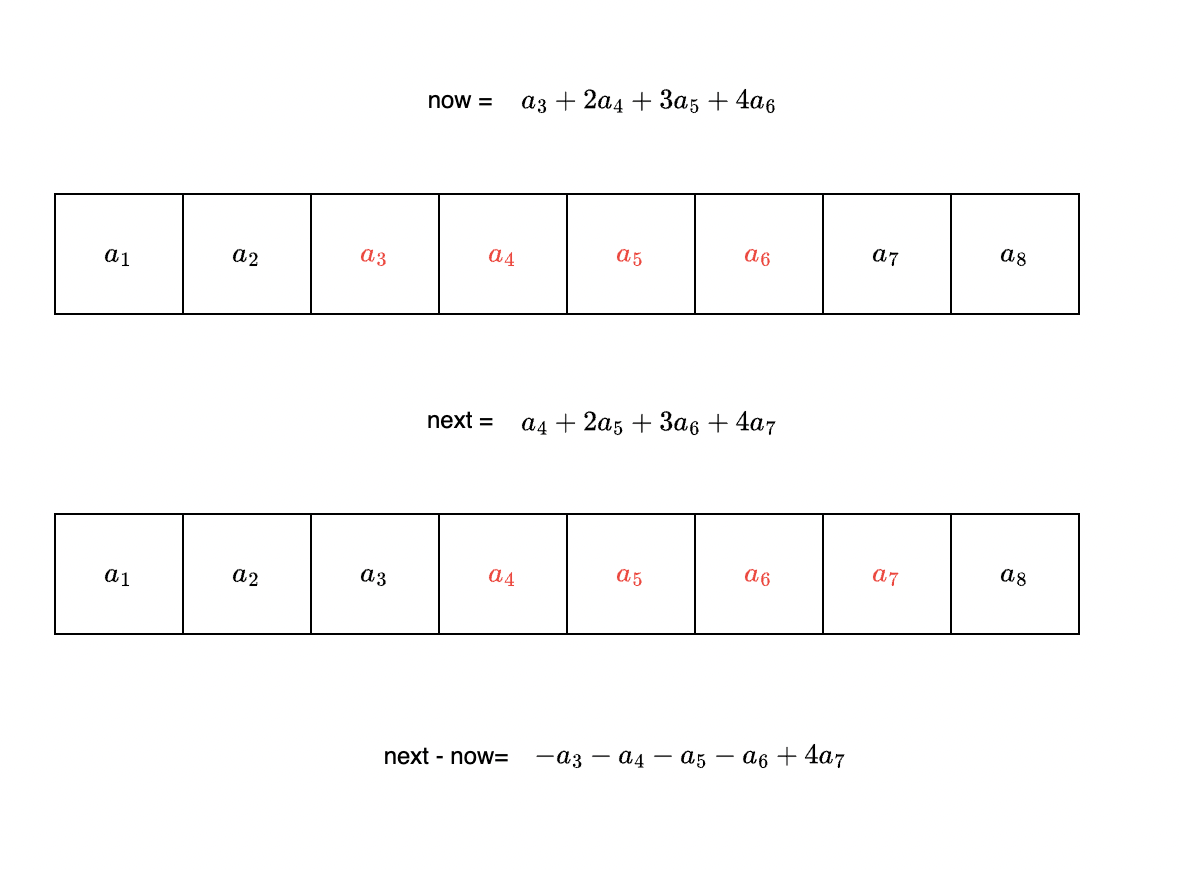
<그림 1. n=8, m = 4인 임의의 경우>

 위 그림 1인 배열이 길이가 8이고, 연속 부분 배열의 길이가 4인 경우를 나타낸 그림이다. 이 때, 현재 now 상황에서 next 상황으로 가는 것을 생각해보면, 결국 추가되는 요소는 $a_7$이고 제거되어야 하는 요소는 $a_3$이다. 따라서, 슬라이딩 윈도우를 통해 이를 만족할 수 있고 복잡도를 $O(N)$으로 낮출 수 있다. 그러나, 문제에서 요구하는 부분 배열 원소들의 합이 최대가 되어야 하므로 항상 현재 부분 배열의 합을 저장해야 한다.

 그런데, 추가하고 제거가 일어나면 원래 있었던 부분 배열의 인덱스가 한 칸씩 앞당겨지므로 이것에 대한 조정이 있어야 슬라이딩 윈도우를 하더라도 정확한 합을 저장할 수 있다. 따라서, 기존에 있던 원소들을 한번씩 빼주고 추가되는 원소도 가중치에 맞게 더해주어야 한다. 이렇게 하면 모든 연속 부분 배열의 합을 정확하게 저장할 수 있고, 나왔던 합들의 최대가 정답이 된다

import sys, collections

# 입력부
n, m = map(int, sys.stdin.readline().split())
arr = list(map(int, sys.stdin.readline().split()))
q = collections.deque()

# now : 현재 큐에 저장된 원소들의 가중치 없는 합을 저장하는 변수
now = 0
# temp : 현재 큐에 저장된 원소들의 가중치 있는 합을 저장하는 변수
temp = 0
ans = -98765432109876543210

# 초기에 m개의 원소를 덱에 저장하면서 now, temp 초기화
for i in range(m):
    now += arr[i]
    temp += (i + 1) * arr[i]
    q.append(arr[i])
    
for i in range(m, n):
    ans = max(ans, temp)
    # 현재 덱의 첫번째 원소를 빼야 하기 때문에 temp에서 now를 뺀다
    temp -= now
    # 현재 큐에서 첫번째 원소를 빼야 하기 때문에 가중치가 없는 합에 대해서도
    # 첫번째 원소의 값만큼 빼준다
    now -= q.popleft()
    # 가중치에 따라 추가되는 원소를 temp에 더해준다
    temp += m * arr[i]
    # 새로 추가된 원소의 값만큼 가중치가 없는 합인 now에 저장한다
    now += arr[i]
    # 실제로 원소를 덱에 저장한다
    q.append(arr[i)
    
# 정답 출력
ans = max(ans, temp)
print(ans)

 

D. Index × A(Not Continuous ver.)

 C번의 파생문제로, 부분 배열의 길이에는 변동이 없으나, 부분 배열이 연속이 아니어도 된다는 점이 차이점이다. 또한 n의 제한이 20만에서 2천으로 줄어들었기에 $ O(N^2) $의 풀이가 가능하다. 비연속적이기 때문에 특정 원소를 정답이 되는 부분 배열에 넣을지 말지가 주된 관심사가 됨을 알 수 있다.

 따라서, 상태 공간을 현재 idx번째 원소의 차례이고, 지금까지 cnt개를 뽑았을 때 얻을 수 있는 부분 배열의 최대 합이라고 정의하자. 따라서 점화식은 아래와 같다

$$ dp[idx][cnt] = max(dp[idx][cnt], dp[idx + 1][cnt + 1] + cnt * arr[idx], dp[idx + 1][cnt + 1] $$

 왜냐하면, 현재 cnt개의 부분 수열을 뽑았을 때, 현재 idx번째의 원소를 넣을 때의 최대 합과 그렇지 않았을 때의 최대 합 중 더 큰것을 재귀적으로 택하면 최종적으로는 가장 큰 합을 구할 수 있기 때문이다. 또한, 현재 상태 공간으로 다시 돌아올 수 없는 DAG 구조이기 때문에 다이나믹 프로그래밍 문제로 귀결됨을 알 수 있다

// pypy3로는 시간초과가 나기 때문에 c++로 첨부
#include <bits/stdc++.h>

typedef long long ll;
using namespace std;

int n, m;
int arr[200001];
// dp : 현재 idx번째 원소의 차례이고, 지금까지 cnt개를 뽑았을 때 얻을 수 있는 부분 배열의 최대 합을 저장하는
//      2차원 상태 공간 배열
ll dp[2001][2001];
ll inf = -987654321098765432;

// go : 현재 idx번째 원소의 차례이고, 지금까지 cnt개를 뽑았을 때 얻을 수 있는 부분 배열의 최대 합을 리턴하는 함수
ll go(int idx, int cnt) {
    // Base Case : 부분 수열을 m개만큼 뽑은 경우
    if (cnt == m) {
        return 0;
    }
    // Base Case : 부분 수열을 m개만큼 뽑지 못했고 배열의 끝에 다다른 경우
    if (idx == n) {
        return inf;
    }
    // Memoization
    if (dp[idx][cnt] != -1) {
        return dp[idx][cnt];
    }
    // 초기화 및 점화식
    dp[idx][cnt] = inf;
    dp[idx][cnt] = max(dp[idx][cnt], max(go(idx + 1, cnt + 1) + (cnt + 1) * arr[idx], go(idx + 1, cnt)));
    return dp[idx][cnt];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    // 입력부
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }
    // 메모리 초기화 및 정답 출력
    memset(dp, -1, sizeof(dp));
    cout << go(0, 0) << "\n";
}

 

E. Erasing Vertices 2

 대회 중에서는 풀지 못했던 문제이다. 다른 문제를 풀던 중 발상이 비슷해보여 적용했더니 업솔빙에 성공하였다. 입력으로 정점의 갯수가 n개, 간선의 갯수가 m개인 그래프가 주어졌을 때 n번에 걸쳐 정점을 삭제하는 문제이다. 단, 하나의 정점을 삭제할 시 해당 정점과 직접적으로 연결된 다른 정점들 중 삭제되지 않은 정점들의 점수의 합만큼이 비용으로 정의된다. 이 때 각각의 연산 시 드는 최대 비용을 최소화하는 문제이다. 

 해당 문제는 그리디 알고리즘과 우선순위 큐를 이용하여 풀었는데 아이디어 자체는 단순하다. 우선 그리디 알고리즘의 정당성부터 살펴보면, 직관적으로 현재 i번째 연산에서 가장 작은 비용을 제공하는 정점을 뽑아야 전체의 최대가 최소화된다는 점이다. 그런데, 현재 정점을 삭제한 이후 다음 정점을 찾으려면 결국 살아있는 정점들을 전부 봐야한다는 문제가 있다. 따라서 단순한 그리디 알고리즘으로는 $ O(N^2) $의 복잡도를 가지게 되고 시간 초과를 피할 수 없다. 

 시간을 낮추기 위해서는 우선순위 큐가 필요하다. 왜냐하면 현재 정점을 삭제한 이후 현재 정점들과 연결된 정점들을 추가해도 결국 다음 연산에서 삭제되는 정점은 전체 큐에서 가장 비용이 낮은 큐만 선택되기 때문이다. 그렇다면 같은 정점이 큐안에 여러번 담길 수 있는 문제가 있고 이는 이미 삭제한 정점을 2번 삭제하는 문제와 이어질 가능성이 있다. 

 따라서, 현재 i번 정점을 삭제할 때 드는 비용을 담는 배열 d를 정의하자. 그렇게 되면 현재 시점에서 삭제한 임의의 정점 i에 대해서 삭제한 비용 $c_i$가 $d[i]$값보다 크거나 같다면 이미 정점 i를 최소 비용을 삭제하였기 때문에 삭제하지 않고 단순히 우선 순위 큐에서 뽑기만 하면 중복 삭제를 해결할 수 있다. 따라서 전체적인 복잡도는 $ O(NlogN) $이 되고 시간안에 정답을 구할 수 있다 

import sys, heapq

# 입력부
n, m = map(int, sys.stdin.readline().split())
arr = list(map(int, sys.stdin.readline().split()))

# adj : 인접 리스트
adj = dict()
for i in range(n):
    adj[i] = set()
    
# cache : 정점들의 삭제 비용을 저장하는 배열
cache = [0] * n
for _ in range(m):
    a, b = map(int, sys.stdin.readline().split())
    a -= 1
    b -= 1
    adj[a].add(b)
    adj[b].add(a)
    cache[a] += arr[b]
    cache[b] += arr[a]
    
q = []
inf = 98765432109876543210

# d : 현재 정점 i를 삭제하기 위해 필요한 비용 중 최소값을 저장하는 배열
d = [inf] * n
for i in range(n):
    heapq.heappush(q, (cache[i], i))
while q:
    # now_dist : 현재 now번 정점을 삭제하려면 드는 비용
    now_dist, now = heapq.heappop(q)
    # 현재 now번 정점을 삭제하는데 드는 비용보다 이전에 정점을 삭제한 비용이 더 적다면 실제로 삭제를 하지 않는다
    if d[now] < now_dist:
        continue
    # 비용 배열 갱신
    d[now] = now_dist
    for next in adj[now]:
        if now in adj[next]:
            # 현재 정점을 인접한 정점에서 삭제
            adj[next].remove(now)
            # 인접한 정점들의 비용에서 현재 정점의 크기만큼 감소
            cache[next] -= arr[now]
            # 인접한 정점들을 우선순위 큐에 삽입
            heapq.heappush(q, (cache[next], next))
            
# 정답 출력
print(max(d))