[Python 3] BOJ - 1929 "소수 구하기"

 # 문제 링크 : https://www.acmicpc.net/problem/1929

1929번: 소수 구하기

 

 # 풀이 :

개인적으로 문제의 핵심은 에라토스테네스의 체를 통해 전처리하는 것이라 생각한다. N,M제한이 백만이므로 미리 백만까지의 소수 리스트를 구한다음, N,M에 따라 출력을 해주면 정답을 찾을 수 있다.

<그림 1. 100까지의 소수 구하는 과정>

 에라토스테네스의 체 알고리즘 과정은 다음과 같다. 예시를 위해 1부터 100까지의 경우만 구한다고 가정하자. 각각의 수가 소수인지를 판별하여 리스트에 넣는다면 비효율적이다. 그렇다면 어떻게 해야할까? 소수의 정의를 생각해보자. '1과 자기자신만을 약수로 갖는 수'이다. 그렇다면 소수의 배수는 무조건 소수가 아니다. 왜냐하면 소수와 다른 수의 곱으로 이루어져 있기 때문이다. 

<그림 2. 100까지 소수를 구하는 과정>

 2는 소수이므로 2를 제외한 2의 모든 배수를 삭제한다. 이 순간 100이하의 2를 제외한 모든 짝수가 제외됨을 알 수 있다. 3도 소수이므로 3의 배수들도 지워보자

<그림 3. 100까지 소수를 구하는 과정>

 4의 배수도 지워야 할까? 그렇지 않다. 4는 이미 2의 배수를 지울 때 삭제되었으므로 5의 배수를 지워야 한다. 이런식으로 범위 안의 모든 소수의 배수를 지운다면 남는 것은 소수밖에 없기 때문에 빠른 시간에 1부터 n까지의 모든 소수를 구할 수 있다.

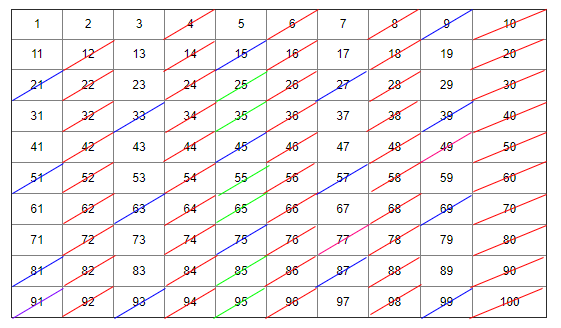
<그림 4. 100까지의 소수>

(그림 상에서 실수로 소수 자신도 삭제하였는데 그림 4가 최종적인 형태이니 참고)

 

 # 코드

import sys
# era : 1부터 num까지의 소수 리스트 리턴
def era(num):
    check = [False] * (num + 1)
    primes = []
    for i in range(2, num + 1):
        if check[i]:
            continue
        j = i * 2
        primes.append(i)
        while j <= num:
            check[j] = True
            j += i
    return primes

pre = era(1000000)
n, m = map(int, sys.stdin.readline().split())
for i in pre:
    if n <= i <= m:
        print(i)