[Python 3] BOJ - 1517 "버블 소트"

 # 문제 링크 : https://www.acmicpc.net/problem/1517

1517번: 버블 소트

 # 풀이:

이 문제는 머지 소트로 푸는 방법과 펜윅 트리(세그먼트 트리)로 푸는 두가지 방법이 있는데 이번 포스팅에서는 펜윅 트리로 풀이할 예정이다. 따라서 개인적으로 이문제의 핵심은 펜윅 트리의 Inversion을 구하는 것이라 생각한다. 이전 버블소트 관련 포스팅은 몇번째 사이클만에 정렬이 완료되는지를 묻는다면 이번 버블 소트 문제는 원소를 바꾼 횟수를 구하는 문제이다.

<그림 1. [4,1,3,2]의 경우>

 그림 1은 [4, 1, 3, 2]의 경우를 나타낸 것이다. 버블 소트에 따라 정렬하게 되면 결과는 [1, 2, 3, 4]가 되고 총 원소를 바꾼 횟수는 4번이다. 그림의 밑줄은 4가지 원소를 정렬하여 넣을 곳이다. 우선 인덱스 0부터 시작하여 빈칸에 차례대로 넣을 것이다.

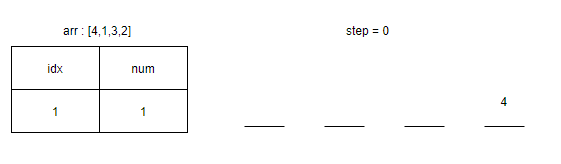
<그림 2. idx = 0인 경우>

 그림 2에서는 그림 1과 달리 step이라는 것이 있는데, 이 step이라는 변수의 의미는 현재 num이 정렬된 배열의 자리, 즉 오른쪽의 올바른 밑줄에 들어가기 위해 거쳐가는 수의 갯수이다. 0번째 인덱스의 4는 빈칸에 들어갈 때 아무런 수가 없었으므로 step은 0이 된다.

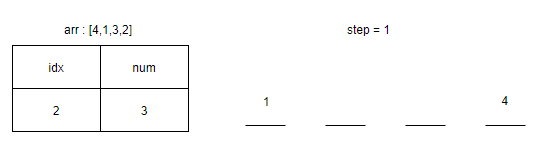
<그림 3. idx = 1인 경우>

 인덱스 1일 때 숫자는 1인데 빈칸에 4가 있었으므로 step에 1을 더해준다. 이 때 빈칸에 들어가는 수와 만나게 되는 수의 쌍의 배열을 p라고 할 때, 1과 4가 만났으므로 p = [(1, 4)]이다.

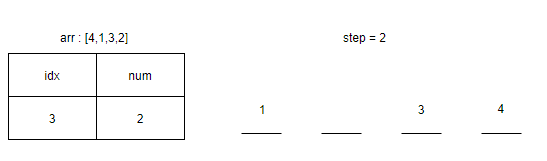
<그림 4. idx = 2인 경우>

 인덱스 2일 때는 숫자 3이 4와 한번 만나므로 step에 1을 더해준다. 또한 새로운 쌍 (3, 4)가 생기므로 p = [(1, 4), (3, 4)]이다.

<그림 5. idx = 3인 경우>

 인덱스 3일 때는 숫자 2와 3,4가 한번씩 만나므로 step에 2를 더해준다. 또한 새로운 쌍 (2, 4), (2, 3)이 생기므로 p = [(1, 4), (3, 4), (2, 4), (2, 3)]이다.

<그림 6. 실제 버블 정렬 시 step과 p>

 그림 1 ~ 5까지의 과정의 결과와 실제 버블 소트 결과인 그림 6은 step과 p가 같음을 알 수 있다. 물론 그림 6에서 p에 더해지는 순서 쌍의 순서와 그림 1 ~ 5까지의 p에 더해지는 순서 쌍의 순서는 다르지만 결과적으로는 p가 같아짐을 알 수 있다. 따라서, p의 원소의 갯수가 곧 step이므로 결과적으로 p가 같아진다면 step도 같아진다.

 그런데 그림 1 ~ 5까지의 과정을 유심히 보면 step에 더해지는 갯수는 현재 들어가야 하는 빈칸 다음 빈칸 부터 마지막 빈칸까지 존재하는 수의 갯수이다. 그런데 어차피 빈칸에 넣을 때는 정렬을 가정하고 넣으므로 현재 빈칸보다 오른쪽에 있는 빈칸은 무조건 현재 빈칸에 들어갈 수보다 크다.

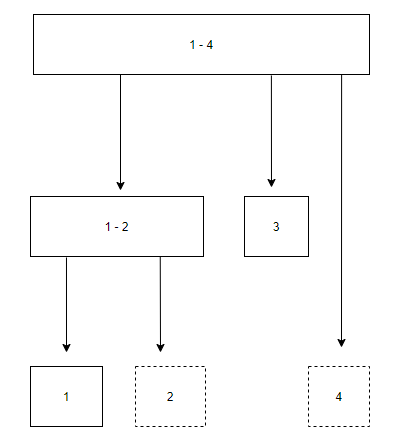
<그림 7. 펜윅 트리>

 간단히 펜윅 트리에 대해 설명하자면 펜윅 트리는 트리로서 각 노드들은 i부터 j까지의 합을 담는다. 점선으로 된 노드는 실제로는 존재하지 않는 노드이다. 왜냐하면 2부터 2까지의 구간을 구하기 위해서는 1부터 2까지의 구간의 합에서 1부터 1까지의 구간을 빼면 되기 때문이다.

 펜윅 트리는 특정 인덱스의 값을 변경하면 그 변경된 값이 상위 노드에도 추가된다. 예를 들어 점선 노드인 2의 값이 현재 3이었는데 5로 바꾼다면 1부터 2까지의 합도 변경이전 보다 2가 커져야 하고, 1부터 4까지, 즉 2가 포함되는 모든 구간의 합이 2만큼 커져야 한다. 

 기본적으로 트리 자료구조이고 비트를 통해 접근하기 때문에 값을 변경하거나 구간합을 구할 때 O(log N)이 걸린다. 이전 단락에서 step을 구한다는 것은 현재 수보다 큰 수의 개수를 찾는 것이라고 하였다. 따라서 리프 노드를 실제 수에 대응한다면 구간 [a + 1, b]의 합이 a보다 큰 수의 갯수가 보장이 된다면 정답을 구할 수 있다. 따라서 현재 수가 a일 때 [a + 1, b]까지의 구간합을 구하고 a를 넣어줘야 하므로 인덱스 a에 1만 추가하면 된다.

<그림 8. 펜윅 트리 예시>

 만일 현재 빈칸에 4만 있는데 2를 빈칸에 넣어야 한다면 순서쌍 (2, 4)가 하나 발생할 것이다. 따라서 2보다 큰 수인 [3,4]의 구간합을 구하면 1이므로 실제 2보다 큰 수와 같다. 그런데 여기서 1만 구하고 2번 노드에 '넣는다'는 의미의 1을 업데이트해주지 않는다면 만약 1을 빈칸을 넣을 경우, 즉 2와 4가 현재 빈칸에 있을 때 1을 빈칸에 넣는 경우에서 1보다 큰 수인 [2,4]의 구간합을 구하면 2가 아니라 1이 되어버리기 때문에 항상 자신보다 큰 수를 구해주고 다 구하면 빈칸에 넣는다는 의미로 해당 노드에 1을 업데이트 시켜준다.

 그런데 우리는 노드를 실제 수에 대응했다고 하였는데 문제에서 배열의 원소는 음수가 될 수도 있다. 그런데 각 원소의 실제 수가 중요한것이 아니라 단순히 대소 관계만 비교하면 되므로 입력으로 들어오는 배열을 상대적인 값으로 바꿔주기만 하면 된다. 즉, 배열이 [-10, -3, 4, 7]로 들어온다면 -10이 첫번째로 크고 -3이 두번째로 크고 4가 3번째로 크고 7이 4번째로 크므로 [1, 2, 3, 4]로 바꿔줘야 펜윅트리를 이용할 수 있다.

 cf) 펜윅트리에 대한 자세한 설명은 여기를 참고하길 바란다.

 

 # 코드

import sys

# fenwick_update : 펜윅 트리인 tree의 idx번째 노드를 d로 갱신하는 함수
def fenwick_update(tree, idx, d):
    while idx <= n:
        tree[idx] += d
        idx += (idx & -idx)

# fenwick_find : 펜윅 트리인 tree의 start번째 노드부터 end번째 노드까지의 합을 리턴하는 함수
def fenwick_find(tree, start, end):
    if end < start:
        return 0
    res = 0
    idx = end
    while idx > 0:
        res += tree[idx]
        idx -= (idx & -idx)
    idx = start - 1
    while idx > 0:
        res -= tree[idx]
        idx -= (idx & -idx)
    return res

# relation_convert : 배열 arr의 원소들을 대소 관계를 유지하는 상대 값으로 바꾼 배열을 리턴하는 함수
def relation_convert(arr):
    sort_arr = sorted(arr)
    mid = dict().fromkeys(sort_arr, 0)
    res = []
    visited = [False] * (len(arr) + 1)
    for idx, temp in enumerate(mid):
        mid[temp] = idx + 1
    for i in arr:
        if visited[mid[i]] == False:
            res.append(mid[i])
            visited[mid[i]] = True
    return res
    
# 입력부
n = int(sys.stdin.readline())
before = list(map(int, sys.stdin.readline().split()))

# after = before의 상대 배열
after = relation_convert(before)

# ftr : 펜윅 트리
ftr = [0] * (n + 1)
ans = 0
for i in range(len(after)):
    # 자신보다 큰 수의 갯수를 ans에 저장하고
    ans += (fenwick_find(ftr, after[i], len(after)))
    # 저장했으면 자신을 넣는다
    fenwick_update(ftr, after[i], 1)
    
# 정답 출력
print(ans)