[Python 3] BOJ - 1149 "RGB 거리"

 # 문제 링크 : https://www.acmicpc.net/problem/1149

1149번: RGB거리

 # 풀이 :

그리디 알고리즘으로 자칫 접급할 수 있지만, 반례를 쉽게 찾을 수 있다. 따라서 이 문제는 그리디 알고리즘으로는 최적해를 찾을 수 없다. 따라서 다이나믹 프로그래밍으로 접근해야 한다. 개인적으로 문제의 핵심은 비록 처음과 끝이 아닌 경우에는 양 옆집과 다른색이 되어야 하지만, 결론적으로 바로 앞집에 의해서만 해당 집의 색깔이 결정된다는 점이다. 

예시)

<그림 1. n = 3인 경우>

 위의 그림 1에서는 설명을 위해 첫번째 집은 빨강, 두번째 집은 초록으로 임의로 설정하였다. 따라서 현재 칠애햐 할 집에 가능한 색깔, 즉 ?는 파랑 혹은 빨강이 되어야 한다. 따라서 우리는 어떤 집을 칠할 때 그 집에 쓸 수 있는 색깔은 바로 앞집에서 쓴 색깔이 아닌 색깔은 모두 가능하다는 것이다.

<그림 2. 일반화>

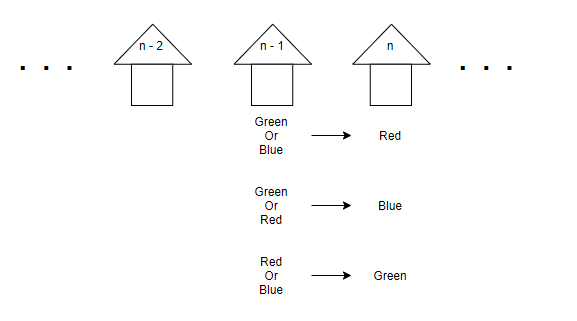
 따라서 일반화를 거친다면, 점화식은 아래와 같다.

따라서 DP 테이블은 1차원이 아니라, N x 3인 2차원 배열이 되어야 한다.

 

 # 코드

import sys

n = int(sys.stdin.readline())

# N x 3 DP Table 생성
# table[i][0] = i번째 집을 빨강으로 칠하는 경우
# table[i][1] = i번째 집을 파랑으로 칠하는 경우
# table[i][2] = i번째 집을 초록으로 칠하는 경우

table = [[0,0,0] for _ in range(n)]

for i in range(n):
    temp = list(map(int, sys.stdin.readline().split()))
    if i == 0:
        table[0] = temp
    else:
        # 점화식을 통한 DP Table 채우기
        table[i][0] = min(table[i - 1][1], table[i - 1][2]) + temp[0]
        table[i][1] = min(table[i - 1][0], table[i - 1][2]) + temp[1]
        table[i][2] = min(table[i - 1][0], table[i - 1][1]) + temp[2]
        
# 빨강, 초록, 파랑으로 칠하는 경우 중 최소값 출력
print(min(table[n - 1]))