[Python 3] BOJ - 2233 "사과나무"

 # 문제 링크

https://www.acmicpc.net/problem/2233

2233번: 사과나무

 

 # 풀이

 개인적으로 이 문제의 핵심은 스택과 LCA라고 생각한다. 크게 보면 문제는 트리를 만들고 썩은 두 사과의 LCA를 파악하는 두 단계로 나누어져있다.

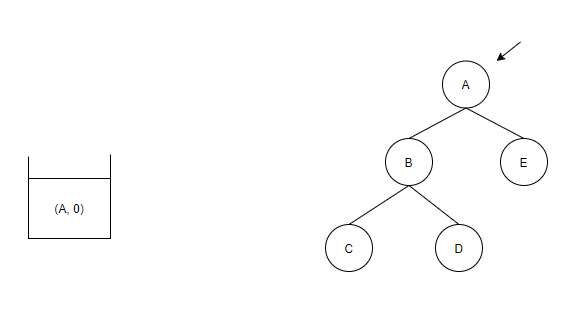
<그림 1. 예제 1의 트리 생성 과정>

 위 그림 1은 스택을 이용하여 트리를 구현하는 그림이다. 문제에서 제시한 바에 따라 0이라면 현재 가리키는 노드가 처음 진입하는 의미이기 때문에 그대로 스택에 추가한다.

<그림 2. 예제 1의 트리 생성 과정>

 위 그림 2는 리프 노드인 C까지 진행된 과정을 나타내는 그림이다. C는 리프 노드이고 더이상 방문할 정점이 없다. 따라서 문제에서 제시한 바와 같이 그 다음에는 노드의 시작이 아닌 노드의 끝인 1이 나올 차례임을 알 수 있다. 따라서, 현재 (C, 0)은 더 이상 스택에 존재해서는 안된다. 따라서 스택에서 pop을 시켜준다.

 그런데, 현재 스택에서 (C, 0) 바로 밑에 존재하는 노드는 B이고 B는 C의 부모 노드이다. 따라서, 현재 보고 있는 이진 수열이 1이라면 스택을 pop하되, 바로 밑의 노드가 부모 노드임을 이용하여 인접 리스트를 작성할 수 있다.

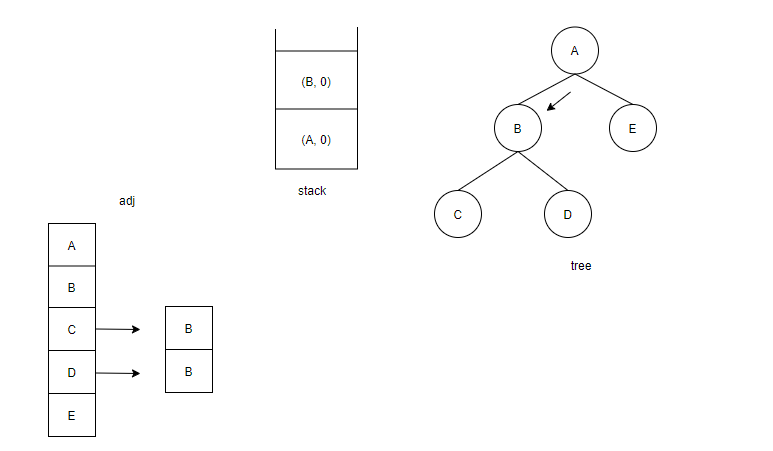
<그림 3. 예제 1의 트리 생성 과정>

  위 그림 3은 그림 2의 논리에 따라 인접 리스트를 구성한 과정 중 일부이다. (C, 1)과 (D, 1)은 직접 스택에 넣지 않고 스택의 top부분이 각각 (C, 0), (D, 0)임이 자명하기 때문에 pop한 후 자신의 바로 밑에 있는 부모 노드로 가는 단방향 인접 리스트를 생성한다. 이렇게 트리를 생성할 수 있다.

<그림 4. LCA>

 위 그림 4는 그림 1에서 그림 3의 과정을 통해 실질적인 인접 리스트를 모두 생성한 이후 어떤 사과를 잘라야 하는지를 나타내는 그림이다. 현재 예제 1을 기준으로 할 때 썩은 사과는 C와 D이다. 현재 인접 리스트는 자식에서 부모로 향하는 모습으로 되어 있기 때문에 임의의 정점에서 DFS를 하게 된다면 임의의 정점의 부모 노드를 포함한 모든 조상 정점을 방문하게 될 것이다. 따라서, 썩은 사과 각각에서 DFS를 실행하게 된 이후 어떤 노드가 2번 이상 방문했다면 바로 그 노드가 공통 조상의 후보가 되는 노드 중 하나임은 자명하다. 그런데, 문제에서 지적한 바와 같이 루트노드를 자르게 된다면 멀쩡한 사과를 많이 버려야 하기 때문에 그러한 공통 조상 후보 중 가장 깊이가 깊은 노드를 잘라야 멀쩡한 사과를 최소한으로 버릴 수 있다.

 

 # 코드

import sys

# dfs : 현재 num 노드에서 루트로 가는 dfs
def dfs(num):
    # 방문하는 조상 정점(자기 자신 포함)의 방문 횟수를 1 증가
    cnt[num] += 1
    for next in adj[num]:
        dfs(next)

# 입력부
n = int(sys.stdin.readline())
arr = list(map(int, sys.stdin.readline().rstrip()))
x, y = map(int, sys.stdin.readline().split())

# st : 스택
# convert : 현재 이진 수열의 위치가 몇번째 정점인지를 나타내는 배열
st = []
convert = [0] * (2 * n)

# num : 정점 번호
num = 0

# adj : 자식에서 부모로 향하는 단방향 인접 리스트
adj = [[] for _ in range(n)]

# cnt : 썩은 사과들이 dfs를 통해 방문하는 횟수를 저장하는 리스트
cnt = [0] * n

# height : 정점의 높이를 저장하는 배열, 작을 수록 루트에 가까움에 주의
height = [0] * n

for i in range(len(arr)):
    # 시작한다면 스택에 추가
    if arr[i] == 0:
        if st:
            # 바로 밑 노드는 부모이므로 높이 1 증가
            height[num] = height[st[-1]] + 1
        st.append(num)
        convert[i] = num
        # 정점 번호 증가
        num += 1
    # 끝난다면 밑 노드(부모 노드)와 인접 리스트로 연결
    else:
        temp = st.pop()
        convert[i] = temp
        if st:
            adj[temp].append(st[-1])

# x, y : 썩은 사과의 정점 번호, 원래는 이진 배열에서의 위치이고 1부터 시작하기 때문에
         1을 빼준 후 위치에서 정점 번호로 convert 리스트를 통해 변환
x, y = convert[x - 1], convert[y - 1]
dfs(x)
dfs(y)

# res : 모든 정점들의 방문 횟수와 깊이, 정점 번호를 저장하는 리스트
res = []
for i in range(n):
    res.append((cnt[i], height[i], i))
    
# 공통 조상 정점은 방문 횟수가 2여야 하고, 그 중에서 가장 깊이가 깊은 것이 정답이므로 정렬
res.sort(key=lambda x : (-x[0], -x[1]))

# 정답 출력
for i in range(len(arr)):
    if convert[i] == res[0][2]:
        print(i + 1, end=' ')