[Python 3] BOJ - 1648 "격자판 채우기"

# 문제 링크 : https://www.acmicpc.net/problem/1648

1648번: 격자판 채우기

# 풀이 :
이 문제를 풀면 타일링 문제들을 쉽게 풀 수 있다. 왜냐하면 BOJ 타일링 문제들은 N혹은 M을 고정시키지만 이 문제는 N과 M이 변하기 때문이다. 개인적으로 이 문제는 비트마스킹을 이용한 다이나믹 프로그래밍이 핵심이라고 생각한다. 우선 다이나믹 프로그래밍인 이유는 어떤 칸을 (i, j)라고 한다면 (i, j - 1)에서 옆으로 채울 수도 있고 (i - 1, j)에서 밑으로도 채울 수 있기 때문이다. 따라서 타일을 어느 방향으로 채우느냐에 따라 부분 문제가 달라지고 이전의 결과로 인해 현재의 문제가 영향을 받기 때문에 다이나믹 프로그래밍의 조건을 만족한다.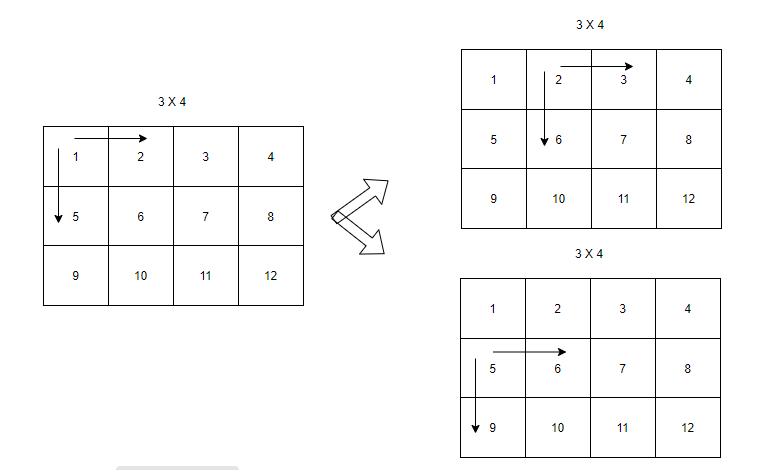

<그림 1. N = 3, M = 4인 경우>

그림 1에서 각 격자판에 번호를 부여하였다. 그런데 이는 3 X 4 2차원 행렬을 (0,0)부터 1차원 배열로 펼쳤을 때 각 원소들의 순서들과 동일하다. 그런데 좌측의 그림에서 밑으로 채우느냐 옆으로 채우느냐에 따라 다음 시작점이 달라지게 된다. 따라서 현재까지 오기 위해 어떤 수를 채웠는지에 대한 상태가 필요하다. 그런데 정해진 상태는 '채운다' 혹은 '채우지 않는다' 2가지 상태가 있으므로 비트마스킹을 이용해야 한다. 그런데 두가지 경우, 즉 1 X 2 혹은 2 X 1로 채우는 경우 + '채운다 or 채우지 않는다'의 4가지 정보를 표현하려면 이진수로는 부족하다. 따라서 어떤 칸이 비어있으면 2 X 1로 채우고 현재 칸에서 오른쪽으로 2번째 칸도 비어있다면 현재칸에서 오른쪽으로 2번째 칸부터 채워나간다. 즉, 실제로 1 X 2를 채우는 것이 아니라 함수의 호출을 2칸씩 해줌으로서 간접적으로 채워나가는 방식을 선택하면 된다

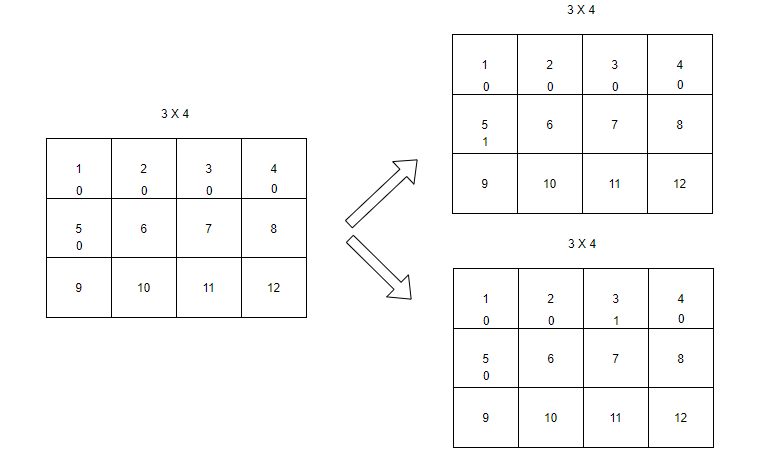
<그림 2. 비트마스킹>

그림 2의 오른쪽 상단 그림은 현재 칸이 1일 때 밑 칸을 2 X 1로 채우는 경우를 비트마스킹으로 나타낸 것이고 오른쪽 하단의 그림은 현재 칸이 1일 때 옆칸을 1 X 2로 채우는 경우를 비트마스킹으로 나타낸 것이다. 이 때 주의할 점은 옆칸을 채우는 경우는 4번째 칸, 8번째 칸, 12번째 칸처럼 한 행의 마지막 칸이라면 채울 수 없으므로 예외 처리를 해야한다는 점과 옆을 채웠다면 현재 칸에서 오른쪽으로 두번째 칸에서 시작해야한다는 것이다. 왜냐하면 현재 칸에서 옆으로 1칸을 채우고 바로 오른쪽으로 첫번째 칸(2번째 칸)에서 시작하게 되면 2번째 칸의 비트는 0이므로 1 ~ 2를 1 X 2로 채우고 다시 2 ~ 3을 1 X 2로 겹치게 채운 경우가 발생하기 때문이다.
따라서 마지막 칸을 채우는 경우 마지막 칸의 비트가 켜져 있지 않다면, 그림을 예시로 들면 12번째 칸이 채워지지 않았다는 것은 11번째 칸에서 옆으로 채운 경우를 의미하므로 이 경우도 세어줘야 한다. 반대로 현재 12번째 칸을 채울 차례인데 12번째 칸의 비트가 켜져있다면, 이전의 8번째 칸에서 밑으로 채운 경우이므로 이 경우는 세어주면 안된다. 왜냐하면 이미 채운 칸이기 때문이다. 추가적으로 현재 채울 칸이 13번째 칸이 될 수 없으므로 이 경우도 세어주면 안되는 것을 Base Case로 세우면 정답을 올바르게 구할 수 있다.

# 코드

import sys

# dp : 2차원 배열로서 i번째 칸이 j번째 비트일 때 채울 수 있는 경우의 수
dp = [[-1] * (1 << 14) for _ in range(14 ** 2)]

# go : 가능한 모든 경우를 리턴하는 함수
def go(num, status):

    # Base Case 1 : 마지막 칸이 안 채워진 경우(=마지막 칸 - 1에서 옆으로 채운 경우)
    if num == n * m and status == 0:
        return 1
        
    # Base Case 2 : 마지막 칸을 넘어가는 경우
    if num >= n * m:
        return 0
        
    # Memoization
    if dp[num][status] != -1:
        return dp[num][status]
    dp[num][status] = 0
    
    # 현재 칸이 채워져있다면
    if status & 1:
        # 옆칸으로 이동
        dp[num][status] = go(num + 1, status >> 1)
        
    # 현재 칸이 안채워져있다면
    else:
        # 일단 밑에 칸을 채우고 옆칸으로 이동
        dp[num][status] = go(num + 1, status >> 1 | 1 << (m - 1))
        # 한 행의 마지막 칸이 아니라면 옆칸을 채우고 옆옆칸으로 이동
        if num % m != m - 1 and status & 2 == 0:
            dp[num][status] += go(num + 2, status >> 2)
    dp[num][status] %= 9901
    return dp[num][status]

# 입력부 및 정답 출력
n, m = map(int, sys.stdin.readline().split())
print(go(0, 0))