[Python 3] BOJ - 1562 "계단 수"

 #문제 링크 : https://www.acmicpc.net/problem/1562

1562번: 계단 수

 # 풀이 :

 문제 풀이에 앞서 비트 연산에 대한 개괄적인 이해를 하고 본 포스팅을 본다면 이해에 도움이 될 것이다. 개인적으로 이 문제의 핵심은 비트마스킹을 이용한 다이나믹 프로그래밍이라고 생각한다. 문제에서 계단 수란 각 자릿수의 차이가 1인 수를 의미하고 특히 0부터 9까지의 수를 모두 사용해야 한다. 추가적으로 0으로 시작하는 수는 없다.

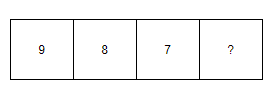
<그림 1. 4자리 계단 수>

 그림 1에서는 앞 세자리는 계단수로 이루어져 있다. 그런데 여기서 4자리 수가 되려면 ?자리에 당연히 6이 들어와야 한다. 그런데 문제에서 입력이 자릿수이고 계단수를 만들기 위해서는 현재까지 어떤 수를 썼으며 다음 단계에 어떤 수로 시작 혹은 끝나야 하는지를 알아야 하기 때문에 총 3가지 정보가 필요하다. 따라서 이 문제의 3차원 행렬 D는 위의 세가지 정보를 담아야 한다. 따라서 3차원 행렬 D[i][j][k]를 현재까지 쓴 수의 정보가 i일 때 자릿수가 j이고 끝나는 수가 k일 때 가능한 경우의 수라고 정의해야 한다.

<그림 2. 6을 추가할 때 비트>

 그림 2는 3차원 배열 D[i][j][k] 중 i에 대한 정보를 담는 것을 나타낸다. 그림 2의 좌측 그림에서 현재까지 사용한 수는 7,8,9이다. 따라서 7,8,9에 해당하는 비트를 1로 쓰고 나머지 수에 대한 비트를 0으로 하면 현재까지 쓴 수에 대한 정보를 표현할 수 있다. 따라서 총 비트 수는 10개가 필요하다. 따라서 오른쪽 그림은 새롭게 6을 썼기 때문에 숫자 6에 해당하는 비트를 1로 바꾸면 된다. 추가적으로 항상 마지막 수를 선택하여 붙여가는 방식으로 계단 수를 만들기 때문에 이미 쓴 수가 0이 되지는 않는다. 또한 0으로 끝난다면 항상 그 다음에는 1로 끝나야 하며, 9로 끝난다면 항상 그 다음에는 8로 끝나야 하는 예외처리를 해주면 정답을 구할 수 있다.

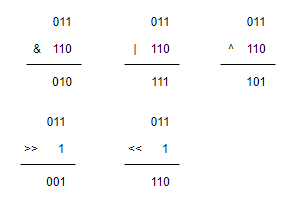
<그림 3. 비트 연산의 예시>

 그림 3은 비트 연산의 예시이다. &(and)연산은 두 비트가 같으면 1, 다르면 0인 연산이고 |(or)연산은 두 비트 모두 0이면 0, 아닌 경우는 1이다. ^(xor)연산은 두 비트가 다르면 1, 같으면 0인 연산이다. >>(right shift)연산은 비트를 오른쪽으로 한칸씩 미는데, 채워지는 왼쪽 비트는 0으로 채우고 원래 자릿수에서 탈락되는 비트는 버린다. 즉, 011의 경우 오른쪽으로 한칸씩 밀면 마지막 1의 경우는 버려지면 01이 되는데 3자리로 맞춰줘야 하므로 001이 된다. <<(left shift)연산은 >>연산과 정확히 반대이다. 

 따라서 그림 2의 경우 6을 추가하는 것은 현재 상황이 1110000000(2)일 때, 0001000000을 추가해야 하므로 or연산을 해주면 된다. 그런데 십진수인 6을 비트로 나타내면 2 ^ 6이므로 right shift 연산을 이용하여 비트로 만들어주고 원래 연산과 or연산을 하면 되므로 (1110000000(2) | (1 << 6))이다.

 

 # 코드

import sys

mod : 나머지 연산을 위해 나눠주는 수
mod = 1000000000

# 자릿수 입력
n = int(sys.stdin.readline())

# dp : 비트 정보, 자릿수, 끝나는 수에 대해 가능한 경우의 수를 담는 3차원 배열
dp = [[[-1] * 11 for _ in range(101)] for _ in range(1 << 11)]

# go : d[f][b][x]를 리턴하는 함수
def go(f, b, x):
    # 끝나는 수가 범위가 넘어가는 경우는 없으므로 0 리턴
    if x < 0 or x > 9:
        return 0
    # 다 뽑았으면
    if b == n:
        # 모든 수를 다 뽑으면 유효한 경우이므로 1 리턴
        if f == (1 << 10) - 1:
            return 1
        # 모든 수를 다 뽑지 않으면 유효하지 않은 경우이므로 0 리턴
        else:
            return 0
    # Memoization
    if dp[f][b][x] != -1:
        return dp[f][b][x]
    dp[f][b][x] = 0
    # 끝나는 수가 0이면 그 뒤에 1만 올 수 있으므로
    if x == 0:
        dp[f][b][x] += go(f | (1 << (x + 1)), b + 1, (x + 1))
        dp[f][b][x] %= mod
    # 끝나는 수가 9면 그 뒤에 8만 올 수 있으므로
    elif x == 9:
        dp[f][b][x] += go(f | (1 << (x - 1)), b + 1, (x - 1))
        dp[f][b][x] %= mod
    # 둘다 아니면 +1, -1만 올 수 있으므로
    else:
        dp[f][b][x] += go(f | (1 << (x + 1)), b + 1, (x + 1))
        dp[f][b][x] %= mod
        dp[f][b][x] += go(f | (1 << (x - 1)), b + 1, (x - 1))
        dp[f][b][x] %= mod

    return dp[f][b][x]

ans = 0

# 각 숫자로 끝나는 모든 경우를 조사해야하므로 각 자리마다 go함수 호출
for i in range(1, 10):
    ans += go(1 << i, 1, i)
    ans %= mod

# 정답 출력
print(ans)