-
[Python 3] BOJ - 1799 "비숍"BOJ 2021. 8. 13. 21:34
# 문제 링크
https://www.acmicpc.net/problem/1799
1799번: 비숍
첫째 줄에 체스판의 크기가 주어진다. 체스판의 크기는 10이하의 자연수이다. 둘째 줄부터 아래의 예와 같이 체스판의 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 체스판 한 줄 단위로
www.acmicpc.net
# 풀이
개인적으로 이 문제의 핵심은 비숍의 특징을 이용한 백트래킹이다. 비숍의 특징은 체스판을 벗어나지 않는 한 대각선으로 원하는 만큼 이동할 수 있다는 것이다. 문제에서 체스판의 최대 길이는 10이고 정사각형이므로 극단적으로 모든 칸이 비숍을 놓을 수 있는 1이라면 $$2^100$$이기 때문에 시간 초과를 피할 수 없어 보인다. 그러나, 비숍을 특징에 따라 모든 방향의 대각선을 검사한다면, 실제 시간은 $$2^100$$보다는 줄어들 것이다.
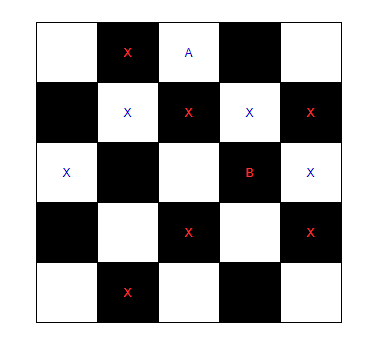
<그림 1. 5 X 5의 경우> 위 그림 1에서 A와 B는 양립함을 알 수 있다. 그런데 A,B뿐만이 아니라 칸의 색깔이 다른 모든 쌍들에 대해서 양립함을 알 수 있다. 따라서, 굳이 모든 칸을 검사하지말고 흰칸과 검은칸으로 나누어 검사하면 시간이 더욱 줄어들 것이다.
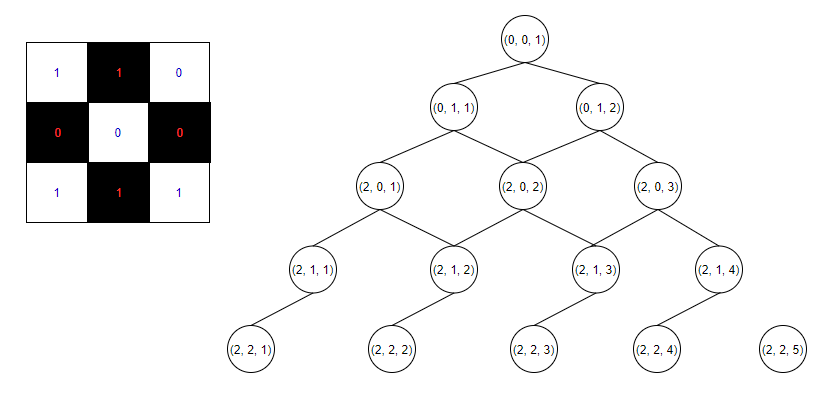
<그림 2. 3 X 3일 때 상태공간> 만일 검은칸과 흰칸을 구분하지 않고 놓을 수 있는 모든 칸을 탐색한다면 그림 2와 같이 될 것이다. 상태 공간의 상태는 (현재 x좌표, 현재 y좌표, 현재까지 놓은 비숍 수)이다. 이 때 마지막 칸인 (2,2)에서는 이전 상태에서 비숍을 추가할 수 없는데, 이유는 맨 처음 (0,0)에 비숍을 놓은 영향을 받기 때문이다.
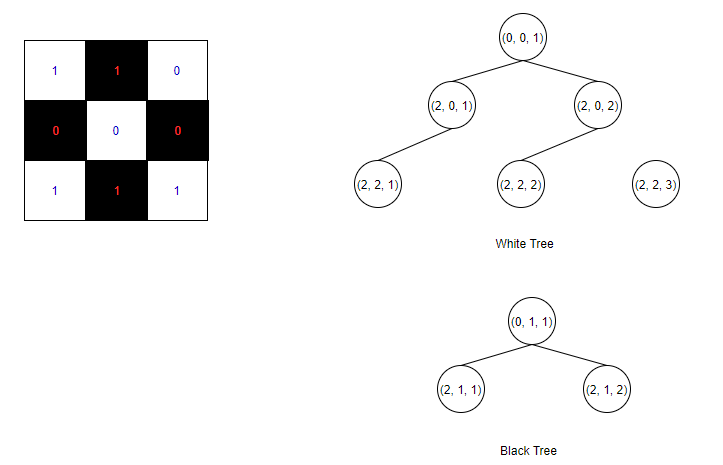
<그림 3. 3 X 3에서의 상태공간> 위 그림은 그림 2에서 흰칸과 검은칸을 구분한 경우의 상태 공간이다. 각각의 트리의 깊이가 상당히 짧아졌으며, 총 상태 공간이 흰 칸의 경우 5개, 검은 칸의 경우 3개로 총 8개이다. 그러나 그림 2에서의 총 상태 공간은 14개이므로 따로 구하는 것이 시간을 더욱 줄일 수 있다. 또한 전체의 경우로 구한 경우나, 흰칸에서의 최대 비숍 수와 검은칸에서의 최대 비숍 수를 더한 경우나 정답에는 차이가 없다.
# 코드
import sys # check : 현재 좌표 (x, y)에서 이전에 놓은 비숍에 영향을 받는지 아닌지를 체크하는 함수 def check(x, y): # 현재 칸이 비숍을 영향을 받으면 놓을 수 없으므로 False 리턴 if temp[x][y]: return False # 그렇지 않다면 놓을 수 있으므로 True 리턴 return True # set : 현재 (x, y)에서 비숍을 놓거나 놓지 않는 함수. 이 때 num은 1 또는 -1로 놓는 경우는 1, 놓았다가 다시 빼는 경우는 -1로 나타낸다 def set(x,y,num): global blank for i in range(n): # 좌상 대각선 nx, ny = x - i, y - i if 0 <= nx < n and 0 <= ny < n: temp[nx][ny] += num # 좌하 대각선 nx, ny = x + i, y - i if 0 <= nx < n and 0 <= ny < n: temp[nx][ny] += num # 우상 대각선 nx, ny = x - i, y + i if 0 <= nx < n and 0 <= ny < n: temp[nx][ny] += num # 우하 대각선 nx, ny = x + i, y + i if 0 <= nx < n and 0 <= ny < n: temp[nx][ny] += num # backtracking : 현재 idx번째 점에서 cnt개의 비숍을 놓는 함수 def backtracking(idx, cnt): global ans # Base Case : 모든 점을 탐색 후 정답 갱신 if idx >= len(grid): ans = max(ans, cnt) return x, y = grid[idx] # 현재 칸에 놓을 수 있다면 backtracking if check(x, y): set(x, y, 1) backtracking(idx + 1, cnt + 1) set(x, y, -1) backtracking(idx + 1, cnt) # 놓을 수 없다면 다음 칸으로 이동 else: backtracking(idx + 1, cnt) # 입력부 n = int(sys.stdin.readline()) arr = [list(map(int, sys.stdin.readline().split())) for _ in range(n)] # temp : 비숍의 영향에 있는지 아닌지를 체크하는 2차원 배열, 0이면 영향에 있지 않고 1이면 영향에 있다 temp = [[0] * n for _ in range(n)] # grid : 놓을 수 있는 좌표의 list grid = [] ans = 0 for i in range(n): for j in range(n): if arr[i][j]: # 흰칸(검은칸)만 담음 if (i + j) % 2 == 0: grid.append((i,j)) # 흰칸(검은칸)에 대해서만 백트래킹 backtracking(0,0) res1 = ans temp = [[0] * n for _ in range(n)] grid = [] ans = 0 for i in range(n): for j in range(n): if arr[i][j]: # 검은칸(흰칸)만 담음 if (i + j) % 2 == 1: grid.append((i,j)) # 검은칸(흰칸)에 대해서만 백트래킹 backtracking(0,0) res2 = ans # 두 경우를 더하여 정답 출력 print(res1 + res2)'BOJ' 카테고리의 다른 글
[Python 3] BOJ - 2536 "버스 갈아타기" (0) 2021.08.17 [Python 3] BOJ - 10800 "컬러볼" (0) 2021.08.16 [Python 3] BOJ - 3078 "좋은 친구" (0) 2021.08.12 [Python 3] BOJ - 2812 "크게 만들기" (0) 2021.08.11 [Python 3] BOJ - 2878 "캔디캔디" (0) 2021.08.10