[Python 3] BOJ - 10800 "컬러볼"

 # 문제 링크

https://www.acmicpc.net/problem/10800

10800번: 컬러볼

 

 # 풀이

 개인적으로 이 문제의 핵심은 누적 합과 lower_bound, 좌표 압축의 적절한 이용이라고 생각한다. 현재 계산해야 하는 공의 색깔이 a이고 무게는 b라고 하자. 이 때, 전체 무게에서 b 이상인 공은 잡을 수 없다. 또한 b 미만이라 하더라도 a색깔인 공도 잡을 수 없기에 전체 무게에서 무게 b 이상의 공의 총 무게와 a 색깔에서 무게 b 미만인 공의 총 무게를 빼주면 정답을 구할 수 있다

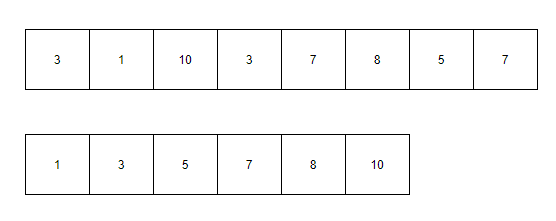
<그림 1. 좌표 압축>

 위 그림 1은 좌표 압축에 대한 간략한 그림이다. 현재 그림 1에서 상단의 그림이 실제 공의 무게에 대한 정보라고 하자. 이 때 각 무게들의 중복을 처리 한 후, 정렬하게 되면 아래와 같은 형태로 바뀌게 된다. 따라서, 현재 그림에서 7은 아래 그림에서 무조건 인덱스 3의 자리에 위치하게 된다. 그러나, 유의해야 할 점은 이렇게 바꾸게 된다면 색깔에 대한 정보를 잃어버린다는 점이다

<그림 2. 좌표 압축을 통한 누적 합>

 위 그림 2는 각각의 무게에 대한 압축된 인덱스끼리 더하는 것을 나타내는 그림이다. 화살표의 같은 색깔은 같은 무게이며 같은 인덱스를 가지게 되고, 인덱스에 자신의 무게를 더해가므로 현재 가장 아래에서 두번째 배열에는 각각의 무게의 합이 된다. 예를 들어 인덱스 3에서는 14인데, 이는 맨 위에서 실제 무게 배열에서 7이 2개 있다는 정보를 나타내는 것이다. 따라서, 가장 아래 배열의 prefix sum을 하게 되면 특정 구간에서의 무게 합을 빠르게 구할 수 있다. 따라서 정답을 구하기 위해 필요한 부분의 첫번째, 즉 b이상의 무게의 총합을 구할 수 있게 되었다. 따라서 두번째 부분, 같은 색상에서의 무게 b미만의 합만 구하면 된다

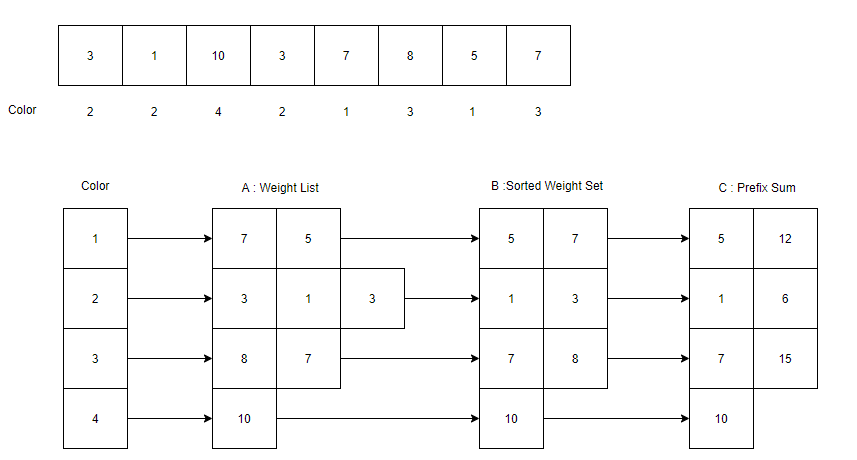
<그림 3. 색깔 별 dictionary를 통한 누적 합>

 위 그림 3은 두번째 부분, 즉 같은 색상에 있어 b미만의 무게의 총합을 찾는 것을 시각화한 그림이다. 각각의 color를 key, 그 때의 weight list를 value로 갖는 dictionary를 만든다. 이것을 A dictionary라고 하자. 이 때, A와 같은 key를 공유하면서, A의 value를 중복 처리를 한 후 정렬시킨 리스트를 value로 갖는 dictionary를 B dictionary라고 하자. 역시 A와 같은 key를 공유하면서, B dictionary의 prefix_sum을 value로 갖는 dictionary를 C dictionary라고 하자. 복잡해보이나 결국 C dictionary는 앞서 본 그림 2의 작업을 단지 색깔 별로 진행한 것에 불과하다. 따라서, 최종적으로는 C dictionary는 그림 2에서 prefix sum을 찾았던 방식과 똑같은 방식으로 prefix sum을 갖는다

 그렇다면, 현재 색상이 2이고 무게가 3인 공은 경우는 정답을 어떻게 찾을 수 있을까? 우선 전체 무게에서 3의 인덱스는 그림 2에서 1임을 알 수 있었다. 이는 lower_bound를 통해 log시간만에 구할 수 있다. 따라서, 3이상의 공의 무게의 합은 전체 무게의 총합 - weight_prefix[1 - 1] = 44 - 1 = 43을 prefix sum을 통해 구할 수 있다. 이 때, 인덱스에서 1을 빼는 이유는 3미만의 무게는 필요가 없기 때문이다

 또한 같은 무게에서 3미만의 무게는 위에서 했던 방식과 같은 방식을 통해, 우선 A dictionary의 2번 키에서 3의 인덱스를 B dictionary를 찾으면 1이 됨을 알 수 있다. 이때도 역시 3미만의 모든 총합을 찾아야 하므로 C dictionary에서 2번 키에서 1 - 1, 즉 0번째 인덱스를 찾으면 1이 됨을 알 수 있다. 따라서 전체 무게의 합인 44에서 3이상의 공의 총합인 43에서 다시 같은 색깔에서 무게 3미만의 총합인 1을 빼면 0이 됨을 알 수 있다. 

 

 # 코드

import sys, bisect

# 입력부
n = int(sys.stdin.readline())

# arr : (공의 색깔, 공의 무게)을 담는 리스트
arr = []

# whole : 전체 무게의 총합
whole = 0

weight = set()

# 각각의 공 입력
for _ in range(n):
    a,b = map(int, sys.stdin.readline().split())
    arr.append((a,b))
    # 전체 무게에 현재 공의 무게를 더함
    whole += b
    # 중복 제거
    weight.add(b)

# 중복 제거 후 정렬
weight = sorted(weight)

# res : 같은 인덱스에서의 총합을 저장하는 리스트(누적 합 아님)
res = [0] * (len(weight) + 1)

# total_pf : 전체 무게 기준 누적 합 배열
total_pf = [0] * (len(weight) + 1)

for i in arr:
    # 현재 무게의 인덱스를 lower_bound를 통해 찾음
    idx = bisect.bisect_left(weight, i[1])
    # 같은 인덱스끼리 더함
    res[idx] += i[1]

# 누적 합 갱신
total_pf[0] = res[0]
for i in range(1, len(weight)):
    total_pf[i] = total_pf[i - 1] + res[i]

# temp : 풀이에서의 A dictionary
temp = dict()
for i in arr:
    if i[0] not in temp:
        temp[i[0]] = [i[1]]
    else:
        temp[i[0]].append(i[1])

# sq : 풀이에서의 B dictionary
sq = dict().fromkeys(temp.keys())
for i in sq:
    sq[i] = sorted(set(temp[i]))
    
# q : 풀이에서의 C dictionary
q = dict().fromkeys(temp.keys())
for i in temp:
    size = len(sq[i])
    # 현재 색깔 i에서 같은 인덱스끼리 무게를 더함 (위에서 res와 같은 역할)
    q[i] = [0] * (size + 1)
    for j in temp[i]:
        idx = bisect.bisect_left(sq[i], j)
        q[i][idx] += j
        
    # pf : 색깔 i에서의 누적합
    pf = [0] * (size + 1)
    pf[0] = q[i][0]
    for j in range(1, size):
        pf[j] = pf[j - 1] + q[i][j]
        
    # 최종적으로 누적 합으로 변경
    q[i] = pf

for i in arr:
    # total_idx : 현재 무게의 전체 무게에 대한 압축된 인덱스
    #             따라서 total_idx보다 작은 인덱스는 현재 무게보다 작다고 할 수 있다
    total_idx = bisect.bisect_left(weight, i[1])
    
    # color_idx : 현재 무게의 같은 색깔에 대한 압축된 인덱스
    #             따라서 color_idx보다 작은 인덱스는 같은 색깔이면서 현재 무게보다 작다고 할 수 있다
    color_idx = bisect.bisect_left(sq[i[0]], i[1])
    
    # 정답 출력
    print(whole - (total_pf[-2] - total_pf[total_idx - 1]) - q[i[0]][color_idx - 1])