[Python 3] BOJ - 17619 "개구리 점프"

 # 문제 링크

https://www.acmicpc.net/problem/17619

17619번: 개구리 점프

 

 # 풀이

 개인적으로 이 문제의 핵심은 정렬과 유니온 파인드라고 생각한다.

<그림 1. 5개의 선분>

 위 그림 1에서는 임의의 5개의 선분이 나타나 있다. 현재 a 선분과 d 선분은 겹쳐져 있지 않지만 점프를 통해서 갈 수 있다. 왜냐하면 a에서 b로, b에서 d로 가면 도착할 수 있기 때문이다. c와 d 역시 마찬가지이다. 그러나, e는 자기자신을 제외한 어느 선분도 도달할 수 없다. 

 선분이 겹친다는 것은 선분 a와 b에 대하여 $A_{start} \leq B_{start} \leq A_{end}$가 성립해야 한다. 그런데, 현재 선분 i에서 올바르게 겹치는 선분을 모두 구하려면 현재 그림1에서의 a와 d처럼 실제로는 겹치지 않지만 중간에 1개 이상의 선분을 거쳐 갈 수 있는 선분을 모두 구해야 한다. 역시 i - 1번째 선분도 마찬가지이다. 따라서, 가장 시작이 빠른 선분에서 시작해야 겹치지 않지만 중간에 1개 이상의 선분을 거쳐 갈 수 있는 선분이 없다는 것이 보장이 되기 때문에 시작점을 기준으로 정렬해야 한다.

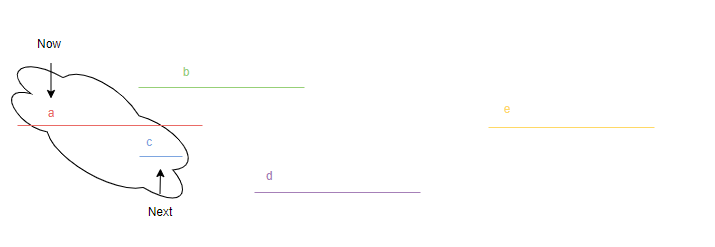
<그림 2, 정렬 후 과정 1>

 위 그림 2에서는 정렬을 한 후의 과정의 일부를 나타낸다. 현재 a 선분을 보고 있고, 그 다음 선분이 c일 때 위에서 본 겹치는 조건에 의해 c에서 a로, 반대로 a에서 c로는 자유롭게 이동할 수 있다. 따라서 a와 c는 어떤 집합으로 묶여 있음을 알 수 있다. 그런데 현재 시작점과 끝점은 선분 a의 시작점과 끝점인데, 이렇게 이동이 가능하다면 새로운 시작점과 끝점으로 갱신해야 할까? 결론은 그럴수도 있고 아닐수도 있다는 것이다. 바꾸지 않아야 하는 경우는 현재 그림 2처럼 c가 a에 완전히 속하는 경우이다. c 다음에 어떤 것이 올지 모르므로 우선적으로 끝점이 최대한 길어야 유리하다. 따라서 바꾸어야 하는 경우는 next 선분의 끝점이 now 선분의 끝점보다 더 먼 경우는 바꾸는 것이 유리하다.

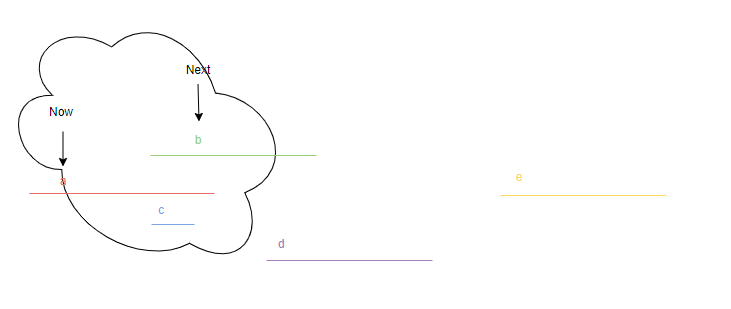
<그림 3. 정렬 후 과정 2>

 따라서 위 그림 3은 그림 2의 이후 과정임을 자연스럽게 알 수 있다. b는 a에서 이동할 수 있으므로 a와 b는 같은 집합에 속하고 현재 시작점과 끝점을 갱신하는 조건을 만족하므로 now를 b로 바꾼다

<그림 4. 정렬 후 과정 3>

 역시 그림 4에서의 d는 선분이 겹치는 조건에 의해 겹치므로 b와 같은 집합에 속하게 된다. 또한 갱신 조건을 만족하므로 d가 다음 now가 된다. 그런데 e는 d와 전혀 겹치지 않으므로 다른 집합에 속하게 된다. 그렇다면 갱신 조건은 어떻게 해야할까? 이 때는 무조건 갱신해야 한다. 그렇지 않는다면 e와 집합으로 묶일 수 있는 선분들을 놓치기 때문이다.

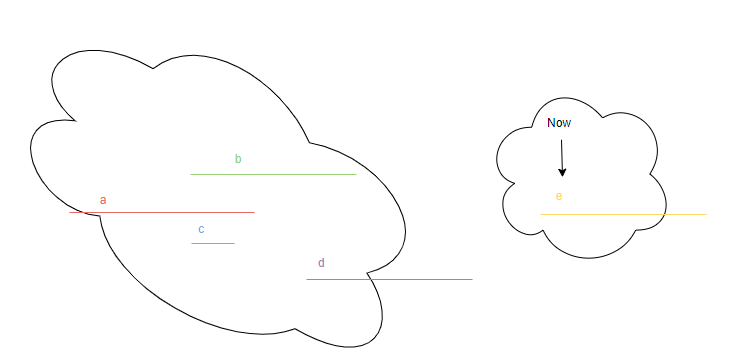
<그림 5. 최종 과정>

 그림 5는 최종 과정까지 끝낸 상태를 나타낸 그림이다. 현재 집합이 2개가 있고 같은 집합에 속한 선분끼리는 자유롭게 오갈 수 있다. 따라서, 두 선분간에 자유로운 이동이 가능한지를 판단할 때 union find를 이용하여 같은 집합이었다면 가능하고, 그렇지 않다면 가능하지 않다.

 

 # 코드

import sys

# find : 현재 x의 parent를 리턴하는 함수
def find(x):
    if x == parent[x]:
        return x
    # 경로 압축
    parent[x] = find(parent[x])
    return parent[x]

# union : x와 y를 같은 집합으로 묶는 함수
def union(x, y):
    x = find(x)
    y = find(y)
    parent[y] = x

# 입력부
n, q = map(int, sys.stdin.readline().split())
arr = []
for i in range(n):
    a,b,c = map(int, sys.stdin.readline().split())
    arr.append((a,b,c,i))
    
# 시작점 기준으로 오름차순 정렬
arr.sort()

# parent : i번의 부모번호를 저장하는 리스트
parent = [i for i in range(n)]

# now_start, now_end, now_idx : 현재 시작점, 현재 끝점, 현재 인덱스
now_start, now_end, _, now_idx = arr[0]
for i in range(1, n):
    # next_start, next_end, next_idx : 다음 시작점, 다음 끝점, 다음 인덱스
    next_start, next_end, _, next_idx = arr[i]
    
    # 겹치는 조건 확인
    if now_start <= next_start <= now_end:
        # 같은 집합으로 묶기
        union(now_idx, next_idx)
        
        # 갱신조건 확인 (끝점이 더 멀어질 수 있는 경우)
        if next_end >= now_end:
            now_start, now_end, now_idx = next_start, next_end, next_idx
            
    # 갱신조건 (겹치지 않는 경우)
    else:
        now_start, now_end, now_idx = next_start, next_end, next_idx
        
 
for _ in range(q):
    a, b = map(int, sys.stdin.readline().split())
    # 만일 a와 b의 부모가 같다면 같은 집합, 그렇지 않다면 다른 집합
    if parent[a - 1] == parent[b - 1]:
        print(1)
    else:
        print(0)