[Python 3] BOJ - 13398 "연속합 2"

 # 문제 링크

https://www.acmicpc.net/problem/13398

13398번: 연속합 2

 

 # 풀이

 개인적으로 이 문제의 핵심은 다이나믹 프로그래밍이라고 생각한다. 우선 수를 하나도 빼지 않고 연속한 수들을 더해 최대값을 구하는 것부터 구해보자.

<그림 1. 원소가 5개인 경우>

 

 위 그림 1은 현재 3을 선택하는 경우를 나타낸다. 문제에서 연속해야한다고 했기 때문에 이전의 -10을 유지한채 3을 더해야 한다. 그런데 이전의 연속합을 무시하고 지금부터 다시 연속합을 만드는 경우도 있다. 따라서, select의 경우는 앞의 연속을 보존한 경우이고, drop은 앞에서의 연속을 무시한채 now부터 새로운 연속을 만드는 경우이다.

<그림 2. select와 drop 통합>

 그런데, 이전의 경우를 무시하는 drop의 경우는 단순히 0을 선택하는것과 같다. 따라서, 0번째 인덱스부터 현재 i번째 인덱스까지의 최대 연속합을 prefix[i]라고 할 때, 그 다음 인덱스의 경우는 prefix[i + 1] = max(0, prefix[i]) + arr[i]이다. 그림을 보면 알 수 있듯, 설령 이전 연속을 버린다하더라도 자기자신은 항상 선택함을 알 수 있다. 똑같은 방식으로 suffix도 나타낼 수 있다. 그러므로, suffix의 정의는 n-1번째 인덱스에서 부터 현재 i번째 인덱스까지의 최대 연속합임을 알 수 있다.

 그런데 왜 이것을 구해야 하나?

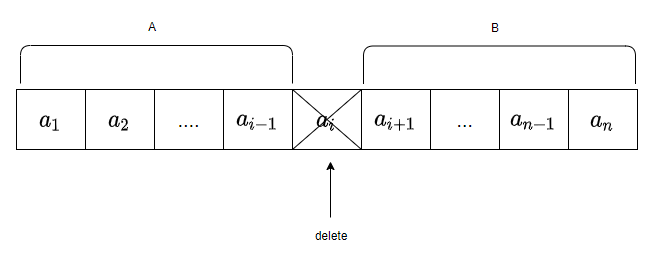
<그림 3. i번째 원소를 삭제하는 경우>

 위 그림 3은 i번째 원소를 삭제하는 경우이다. 이렇게 된다면 $a_{i-1}$과 $a_{i+1}$은 서로 붙일 수가 있다. A는 인덱스 0부터 인덱스 i-1까지 $a_{i-1}$을 반드시 포함한 최대 연속합이고, B는 인덱스 i+1부터 인덱스 n-1까지 $a_{i+1}$을 반드시 포함한 최대 연속합이면 두 구간을 서로 합할 수 있다. 그런데, 정확히 A와 prefix, B와 suffix는 일치하고 각각은 인덱스로 접근하기 때문에 O(1)만에 구할 수 있다. 따라서, 하나도 삭제하지 않는 경우의 최대와 각 인덱스를 삭제했을 때 합친 두 구간의 경우를 비교하면 정답을 구할 수 있다. 주의해야 할 점은 배열의 원소가 음수가 될 수 있기 때문에 dp배열의 초기값을 음의 무한대로 설정해야 한다.

 

 # 코드

import sys

# 입력부
n = int(sys.stdin.readline())
arr = list(map(int, sys.stdin.readline().split()))

# prefix_dp : 0부터 i번째 인덱스까지의 최대 연속 누적합 (반드시 i포함)
prefix_dp = [-9876543210] * (n + 1)

# suffix_dp : i번째 인덱스부터 n-1번째 인덱스까지의 최대 연속 누적합 (반드시 i포함)
suffix_dp = [-9876543210] * (n + 1)

prefix_dp[0] = arr[0]
suffix_dp[-2] = arr[-1]

# 점화식
for i in range(1, n):
    prefix_dp[i] = max(0, prefix_dp[i - 1]) + arr[i]
for i in range(n - 2, -1, -1):
    suffix_dp[i] = max(0, suffix_dp[i + 1]) + arr[i]
    
# 아무것도 삭제하지 않는 경우부터 최대값을 구한다
ans = max(prefix_dp)

# 각 인덱스를 삭제했을 때 합쳐지는 두 구간의 합과 비교
for i in range(n):
    left = prefix_dp[i - 1]
    right = suffix_dp[i + 1]
    ans = max(ans, left + right)
    
# 정답 출력
print(ans)