[Python 3] BOJ - 1722 "순열의 순서"

  # 문제 링크 : https://www.acmicpc.net/problem/1722

1722번: 순열의 순서

 

 # 풀이 :

 개인적으로 문제의 핵심은 분할정복이라고 생각한다. 물론 분할정복 없이도 풀 수 있다. 구현해야 함수가 2개인데, 이 중 어떤 순열이 몇번째 순열인지 판별하는 것은 쉽다. 그러나 개인적으로는 특정 위치의 순열을 구하는 것이 조금 더 어렵다고 생각한다.

<그림 1. N = 4인 순열의 일부>

 현재 n = 4인 순열의 경우를 고려한다고 가정하자. 그런데 가장 앞자리만 놓고 본다면, 그 수는 항상 1,2,3,4 중 하나의 수임은 자명하다. 그런데 1로 시작하는 순열의 갯수는 6개이고, 2로 시작하는 순열의 갯수도 6개이고 3과 4로 시작하는 순열도 6개임을 알 수 있다.

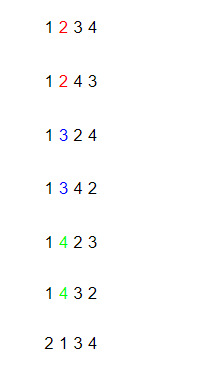
<그림 2. N = 4인 순열의 일부>

 그림 1에서는 순열의 맨 앞자리의 경우만 고려하였다. 그림 2에서는 두번째 자리의 경우만 고려한다고 가정하자. 두번째 자리를 이루는 수는 첫번째 자리 수를 이루는 수를 제외한 모든 수임은 자명하다. 즉, 첫번째 자리 수가 1로 시작하는 어떤 순열이라면, 두번째 수는 반드시 2,3,4 중 하나라는 것이다. 이 때 첫번째 자리가 1이면서 두번째 자리가 2로 시작하는 순열의 갯수는 빨간색의 갯수, 즉 2개이고, 마찬가지로 3과 4도 각각 2개 (파란색, 초록색)이다.

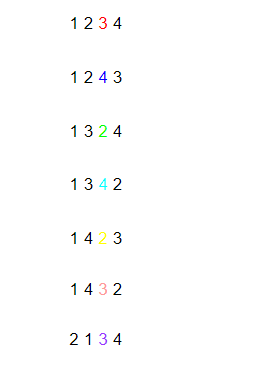
<그림 3. N = 4인 순열의 일부>

 그림 2에서는 순열의 두번째 자리만 고려하였다. 그림 3에서는 순열의 세번째 자리만 고려한다고 가정하자. 세번째 자리를 이루는 수는 첫번째와 두번째 자리수를 제외한 나머지 두 수임은 자명하다. 즉, 첫번째 수로 1, 두번째 수로 2를 쓴다면 세번째에 올 수 있는 수는 3 혹은 4라는 것이다. 이 때 첫번째 자리가 1이면서 두번째 자리가 2이고 세번째 자리가 3으로 시작하는 순열의 갯수는 단 하나이다. 마찬가지로 첫번째 자리가 1이면서 두번째 자리가 2이고 세번째 자리가 4로 시작하는 순열의 갯수도 하나이다. 따라서 모든 경우에 있어 세번째 자리는 무조건 단 한가지의 경우만 가진다.

 정리하면, 첫번째 자리일 때 가능한 가짓수는 6가지, 두번째 자리일 때 가능한 가짓수는 2가지, 세번째 자리일 때 가능한 가짓수는 1이다. 즉, 순열의 길이가 n이고 현재 i번째 자리라면 가능한 가짓수는 (n - 1)!과 같다.

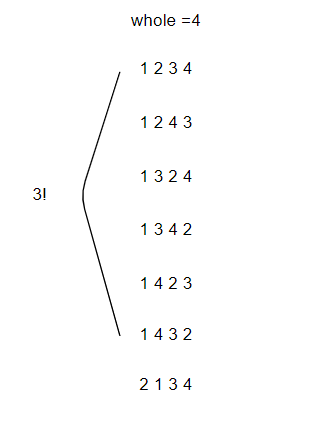
<그림 4. N = 4, K = 7인 경우>

 따라서 현재 수열의 길이가 4이고 찾아야 하는 수열의 위치가 7번째라면, 1로 시작하는 집합의 갯수는 6개이다. 따라서 현재 찾고자 하는 위치는 현재 집합보다 크므로 굳이 첫번째 수가 1로 시작하는 수열을 찾을 이유는 없다. 이때 우리는 첫번째 자리가 2로 시작하는 어떤 순열 중 하나임은 알 수 있다.

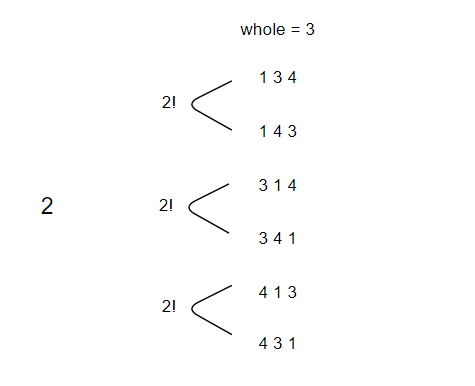
<그림 5. N = 4, K = 7인 경우>

 현재 우리는 첫번째 수는 어떤 수로 시작하는 지 알 수 있다. 그런데 첫번째 수를 얻기 위해 6개의 수를 모두 고려하지 않았다. 따라서 현재 K는 7이 아니라 7에서 6을 뺀 1이다. 즉, 첫번째 수가 2로 시작하는 순열 중에서는 첫번째 순열이라는 것이다. 그런데 두번째 숫자가 1로 시작하는 순열의 가짓수는 2개이고 현재 찾고자 하는 위치는 현재 집합보다 크지 않으므로 두번째 숫자는 1로 시작하는 순열 중 하나임을 알 수 있다.

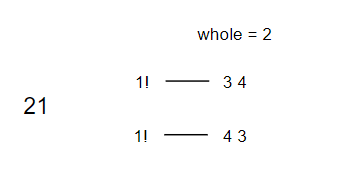
<그림 6. N = 4, K = 7인 경우>

 마찬가지로 현재 K는 두번째 수를 얻기 위해 고려하지 않은 수가 없으므로 K는 이전 단계의 1로 유지된다. 즉, 첫번째 수가 2로 시작하고 두번째 수가 1로 시작하는 순열 중에서는 첫번째 순열이라는 것이다. 그런데 세번째 숫자가 3으로 시작하는 순열의 가짓수는 1개이고 현재 찾고자 하는 위치는 현재 집합보다 크지 않으므로 세번째 숫자는 3으로 시작하는 순열 중 하나임을 알 수 있다.

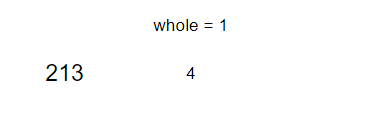
<그림 7. N = 4, K = 7인 경우>

 현재 하나의 수가 남았다면 굳이 우리는 그림 4 ~ 그림 6까지의 과정을 반복할 이유가 없다. 왜냐하면 필연적으로 남은 수는 현재까지 쓴 수에서 쓰지 않은 수이기 때문이다. 따라서 이 작업을 처리한다면 정확히 N개의 길이를 갖는 순열들 중에서 K번째에 위치한 순열을 알 수 있다. 

 이것을 구하기 위해 각 자리수가 몇번째 집합인지를 저장한다면, base case인 whole이 1일 때, 직접적인 순열을 구할 수 있다. 즉, 첫번째 자리는 2였고, 첫번째 자리에 올 수 있는 수는 [1,2,3,4]이었으므로 2는 2번째 집합이라는 것이다. 역시 두번째 자리는 1이었고, 두번째 자리에 올 수 있는 수는 [1,3,4]이었으므로 1은 1번째 집합이라는 것이다. 마지막으로 세번째 자리는 3이었고, 세번째 자리에 올 수 있는 수는 [3,4]이었으므로 3은 1번째 집합이라는 것이다. 이후 whole이 1일때, 즉 한자리를 제외하고 모든 자릿수를 알고 있다면 각 집합에 대응되는 숫자를 알 수 있다.

 반대로 어떤 순열이 주어질 때 이것이 몇번째 순열인지를 알기 위해서는 정확히 이 과정의 역순으로 진행하면 구할 수 있다. 간략히 설명하면 현재 순열이 주어졌기 때문에 각 자리수가 몇번째 집합인지를 먼저 구할 수 있다. 예를 들어, N이 4이고 순열로 2134가 주어진다면, 마지막 자리를 제외하고 (4를 제외) 얻을 수 있는 각 자리수에 대응되는 집합은 [2,1,1]이다. 따라서 리스트의 원소를 순회하면서 (whole - 1)! * (list[i] - 1)을 더해주면 정답을 구할 수 있다. 왜냐하면 (whole - 1)!은 앞에서 보았듯이 한 집합이 차지하는 원소의 갯수이고 그렇게 무시한 집합들은 list[i] - 1만큼 존재하기 때문에 이때까지 무시한 모든 순열의 갯수의 합이기 때문이다.

 

 # 코드

import sys, math

# divide : 순열의 길이가 whole이고 num번째인 순열을 출력하는 함수
# 		   basket : 집합번호를 담는 리스트
def divide(num, whole, basket):
	# 한자리를 빼고 다 뽑은 경우
    if whole == 1:
    	# vis : 중복을 막기 위해 방문체크하는 배열
        vis = [False] * (n + 1)
        # permu : 실제 수열
        permu = []
        # 각 자리수별 집합 번호를 순회한다
        for i in ans:
        	# cnt : 몇번째 집합인가를 판단하는 변수
            cnt = 0
            for j in range(1, n + 1):
            	# 현재 수가 한번도 방문하지 않았다면 cnt 증가
                if vis[j] == False:
                    cnt += 1
                # 현재 j의 집합 번호가 현재의 집합번호와 같다면 실제 순열에 j를 추가한 후
                # 반복문을 빠져 나온다
                if cnt == i:
                    permu.append(j)
                    vis[j] = True
                    break
        # 한번도 사용하지 않은 수가 수열의 마지막 자리이므로 더한다
        for i in range(1, n + 1):
            if vis[i] == False:
                permu.append(i)
        # 실제 순열 출력
        print(' '.join(map(str, permu)))
        return
    # 아직 다 뽑지 않았다면 한 집합의 크기(temp)를 미리 구한다
    temp = math.factorial(whole - 1)
    # 만일 num이 나누어 떨어지지 않는다면, num번째 순열이 속한 집합번호는
    # 1을 추가해야 한다
    if num % temp:
        nth = num // temp + 1
        # 집합번호가 정해졌기 때문에 basket에 추가한다
        basket.append(nth)
        # 무시해야 하는 집합들만큼 num을 건너뛰고 다음 자리수로 이동한다
        divide(num - (nth - 1) * temp, whole - 1, basket)
    # 그렇지 않다면, num번째 순열이 속한 집합번호는 집합의 크기로 나눈 값과 같다
    else:
        nth = num // temp
        basket.append(nth)
        divide(num - (nth - 1) * temp, whole - 1, basket)

# merge : 순열 p가 주어질 때 몇번째 순열인지 출력하는 함수
def merge(p):
    # permu : divide의 basket과 같은 역할을 한다. 즉, 집합 번호를 담는 리스트이다
    vis = [False] * (n + 1)
    permu = []
    for i in range(n - 1):
        cnt = 0
        for j in range(1, n + 1):
            if vis[j] == False:
                cnt += 1
                if j == p[i]:
                    permu.append(cnt)
                    vis[p[i]] = True
                    break
    # order : 몇번째 순열인지 저장하는 변수
    order= 0
    whole = n - 1
    # 순열의 길이를 줄여주면서 (이때까지 무시했던 집합의 갯수) * (집합의 크기)를 더해준다
    for i in permu:
        order += math.factorial(whole) * (i - 1)
        whole -= 1
    # 순열 리스트인 p가 0 base-indexed이기 때문에 최종 정답으로 1을 추가한다
    print(order + 1)

# 입력부
n = int(sys.stdin.readline())
info = list(map(int, sys.stdin.readline().split()))
ans = []

# 정답 출력
if info[0] == 1:
    divide(info[1], n, ans)
else:
    merge(info[1:])