-
[Python 3] BOJ - 9663 "N-Queen"BOJ 2021. 7. 1. 22:47
# 문제 링크 : https://www.acmicpc.net/problem/9663
9663번: N-Queen
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다. N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
# 풀이 :
개인적으로 이 문제의 핵심은 각 열(행)과 대각선을 효율적으로 처리하는 것이라 생각한다. 우선적으로 퀸이 어떻게 움직이는 지 알아보자
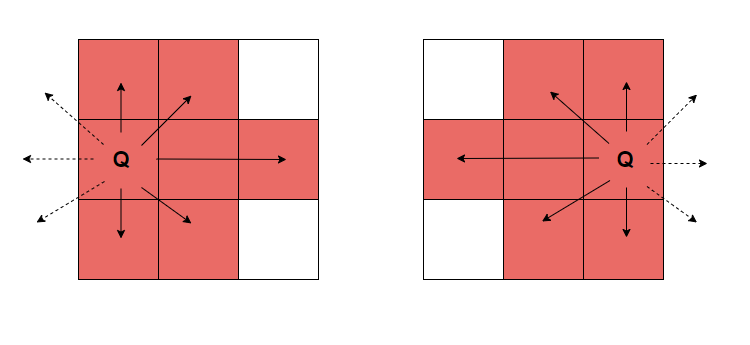
<그림 1. 3X3에서 퀸의 움직임> 위 그림과 같이 퀸이 존재하는 칸을 기준으로 해당 행,열, 4방향 대각선에는 다른 퀸을 놓을 수 없다. 따라서, 만일 행을 기준으로 생각한다면, i번째 행에 하나의 퀸을 놓는다면 (이 때 어느 열인지는 중요하지 않다) i번째 행에 또다른 퀸을 놓는 것은 당연히 불가능하다. 열을 기준으로 생각해도 마찬가지이나, 이번 포스팅에서는 행을 기준으로 하겠다.
그렇다면 해당 행에 퀸을 놓을 수 있는지 없는지는 모든 열이 다른 퀸의 영향에 없어야 하며, 역시 4방향 (우상, 우하, 좌상, 좌하) 모든 대각선의 모든 칸들이 다른 퀸의 영향에서 자유로워야 한다. 반대로 이미 놓여진 퀸들 역시 지금 놓는 퀸의 영향에서 벗어난 상태여야 한다.
따라서, 지금 퀸을 놓을 때 다른 퀸들이 행으로 또는 대각선으로 점유하는지, 그렇지 않는지를 판단했을 때 둘 다 점유하지 않는다면 (i, j) 좌표에서는 퀸을 놓아도 된다. 단순하게는 모든 좌표를 돌면서 확인하는 방법이 있으나, 효율적이지 않다. 어떻게 하면 효율적으로 판단할 수 있을까?

<그림 2. 행에 대한 표현> 위 그림 2에서 왼쪽 그림은 퀸이 (2,0)에 있을 때 퀸의 영향을 받는 칸을 나타내는 그림이다. 가운데 그림은 각 열을 나타낸 그림이다. 각 열마다 색깔이 다르며, 왼쪽 그림과 다르게 행 좌표가 나타나 있지 않다. 왜냐하면 열을 나타내는 데 행의 좌표는 필요없기 때문이다. 마지막 오른쪽 그림은 더 압축된 모습으로, 각 인덱스가 열 자체를 의미한다. 왜 굳이 2차원을 두고 1차원으로 차원을 줄이느냐 하면, 어차피 퀸을 놓는 순간 해당 열 전체는 영향에 들어가기 때문이다.
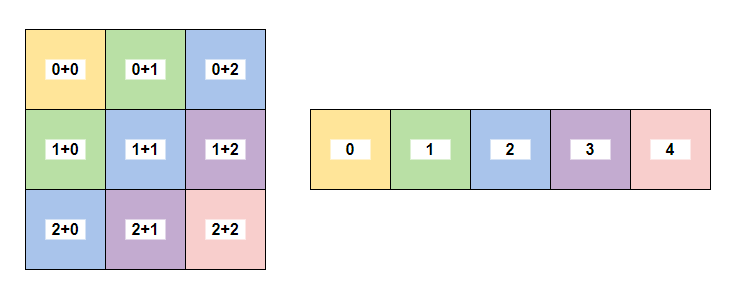
<그림 3. 대각선에 대한 표현 1> 위 그림 3의 왼쪽 그림은 대각선 중 한 방향에 대한 그림이다. 같은 방향의 대각선 칸들끼리는 색깔이 같다. 이 때, 각 좌표의 합이 같다면 같은 대각선 방향임을 알 수 있고, 열과 마찬가지로 2차원을 1차원으로 줄임으로서 모든 칸들에 대한 대각선 상태를 나타낼 수 있다.

<그림 4. 대각선에 대한 표현 2> 위 그림 4의 왼쪽 그림은 대각선 중 한 방향에 대한 그림이다. 같은 방향의 대각선 칸들끼리는 색깔이 같다. 이 때, 각 좌표의 차가 같다면 같은 대각선 방향임을 알 수 있고, 열과 마찬가지로 2차원을 1차원으로 줄임으로서 모든 칸들에 대한 대각선 상태를 나타낼 수 있다. 그런데, 그림 3과 달리 실제 차와 인덱스값이 대응이 되지 않는 문제가 발생한다. 따라서, 인덱스 값에 대응되기 위해 N - 1을 더해준다.
따라서, 최종적으로 (2,0)에 퀸을 놓았을 때의 상태는 아래 그림과 같아진다고 할 수 있다
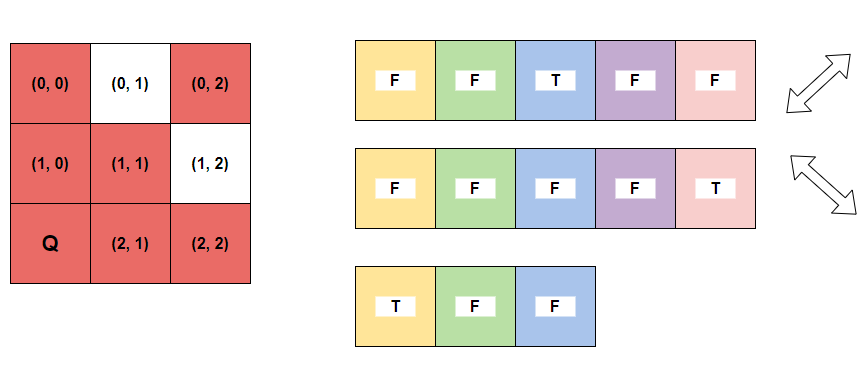
<그림 5. (2,0)일 때 각 방향의 상태> 위 그림 5에서 해당 방향의 모든 칸들이 퀸의 영향 아래에 있다면 True, 하나의 칸이라도 영향을 받지 않는다면 False도 나타내었다. 따라서 실제로 퀸의 영향에서 자유로운 (0, 1)을 기준으로 본다면, 첫번째 대각선 리스트(우상 ~ 좌하) 방향 기준으로는 1이며 F이다. 두번째 대각선 리스트(좌상 ~ 우하) 방향 기준으로도 역시 1인데, F이다. 마지막으로 얄을 기준으로는 1이고, 역시 F이므로 모든 방향을 보아도 현재 퀸의 영향 아래에 있지 않다.
반대로 퀸의 영향 아래에 있는 (0, 2)를 기준으로 본다면, 첫번째 대각선 리스트 방향 기준으로 2이며 T이기 때문에 다른 두 방향이 F라 하더라도 현재 퀸의 영향 아래에 있다.
그런데 우리가 고려하지 못한 방향이 하나가 더 있는데, 바로 행 기준이다. 이유는 간단하다. 백트래킹을 통해 행은 상태 공간으로서 단순히 다음 행으로 넘겨주기만 하면 고려할 수 있기 때문이다.
# 코드
import sys # 입력부 n = int(sys.stdin.readline()) # col : 열 방향 리스트 col = [False] * n # diag1 : 대각선 방향 (우상 ~ 좌하) 방향 리스트 diag1 = [False] * (2 * n - 1) # diag2 : 대각선 방향 (좌상 ~ 우하) 방향 리스트 diag2 = [False] * (2 * n - 1) ans = 0 def go(i): global ans # base case : 모든 행이 조건을 만족했을 경우 if i == n: ans += 1 return # recursive case : 현재 i행에 대해 j열에서 퀸을 놓을 수 있는지 체크 for j in range(n): # 만일 세 방향(열, 대각선1, 대각선2) 모두 다른 퀸들의 영향 밖이라면 재귀 호출 if not col[j] and not diag1[i + j] and not diag2[i - j + n - 1]: # 현재 (i,j)에 의해 각 방향별로 영향을 받는 칸들을 True로 바꿈 col[j] = True diag1[i + j] = True diag2[i - j + n - 1] = True # 재귀 호출 go(i + 1) # backtrack col[j] = False diag1[i + j] = False diag2[i - j + n - 1] = False # 함수 호출 및 정답 출력 go(0) print(ans)'BOJ' 카테고리의 다른 글
[Python 3] BOJ - 2933 "미네랄" (0) 2021.08.03 [Python 3] BOJ - 14395 "4연산" (0) 2021.08.02 [Python 3] BOJ - 1744 "수 묶기" (2) 2020.09.16 [Python 3] BOJ - 1722 "순열의 순서" (0) 2020.09.15 [Python 3] BOJ - 1707 "이분 그래프" (0) 2020.07.08